


 المحاسبة
المحاسبة 
 ادارة الاعمال
ادارة الاعمال
 الادارة
الادارة
 وظيفة التخطيط
وظيفة التخطيط 
 وظيفة التنظيم
وظيفة التنظيم
 وظيفة التوجيه
وظيفة التوجيه 
 وظيفة الرقابة
وظيفة الرقابة 
 ادارة الانتاج
ادارة الانتاج
 ادارة الجودة
ادارة الجودة 
 الادارة الاستراتيجية
الادارة الاستراتيجية
 ادارة التسويق
ادارة التسويق
 ادارة الموارد البشرية
ادارة الموارد البشرية 
 علوم مالية و مصرفية
علوم مالية و مصرفية
 المالية العامة
المالية العامة 
 الاقتصاد
الاقتصاد
 الأحصاء
الأحصاء|
أقرأ أيضاً
التاريخ: 29-6-2016
التاريخ: 29-6-2016
التاريخ: 29-6-2016
التاريخ: 29-6-2016
|
5 - 9 - 13 مخطط التبعثر
يسمى بـ مخطط الانتشار أيضاً ويعرف بأنه مخطط يوضح العلاقة السببية بين متغيرين أحدهما يكون مقياس الجودة لأحد المنتجات والآخر هو العنصر الذي يُعتقد أنه السبب لقيمة هذا المقياس .
يربط مخطط التبعثر بين نوعين من البيانات ويوضح العلاقة بين :
• سبب وتأثير .
• سبب وسبب آخر .
• سبب من جهة وسببين من جهة أخرى .
تبرز فائدة المخطط بالنقاط الاتية :
• تقليص النفقات والوقت اللازم لإجراء الفحص والاختبار.
• استبعاد الفحوصات غير المجدية واستبدالها بأخرى فعالة.
• القيام بضبط العمليات الفعالة على أساس النتائج المتحققة في ضوء العلاقة بين الجودة وخصائص المخرجات .
عادة ما يُقاس مدى الارتباط بين نوعين مختلفين من البيانات في مخططات التبعثر بإحدى الطرائق الآتية :
أ. حساب معامل الارتباط Coefficient of Correlation .
ب. ورقة الاحتمالية Binomial Probability Paper .
ج. أسلوب القيم الوسطية Media Method والتي تعتبر الأكثر شيوعاً .
توضح مخططات التبعثر كما اسلفنا العلاقة بين متغيرين احدهما يؤثر بالآخر ، فإذا كانت العلاقة بين المتغيرين قوية فعند رسم هذين المتغيرين على ورقة بيانية سوف تتجمع هذه التقاط قريبة على بعضها ، أما إذا لم تكن هنالك صلة بين المتغيرين فان النقاط التي تمثل هذين المتغيرين سوف تكون متبعثرة أو منتشرة .
خطوات اعداد مخطط التبعثر
1. جمع بيانات عن المتغيرين (y , x) المزمع دراسة العلاقة بينهما .
2 . ايجاد الوسط الحسابي للمتغير x وذلك بقسمة مجموع قيم هذا المتغير على عددها، ونفس الشيء بالنسبة للمتغير y .
3. رسم محورين احدهما افقي لتمثيل المتغير X والثاني عمودي لتمثيل المتغير y وتدریـج كل محور الى اجزاء متساوية.
4. تأشير قيمة المتغيرات (y , x) على الرسم .
5. تعيين الوسط الحسابي للمتغير X على محوره ورسم خط عمودي من هذه النقطة موازیاً لمحور y .
6. تعيين الوسط الحسابي للمتغير y على محوره ورسم خط أفقي من هذه النقطة موازياً لمحور X . بعد هذا يتشكل لدينا اربع اجزاء يتم ترقيمها من 1-4 عكس اتجاه عقارب الساعة وكما يلي :
7. نجمع النقاط التي تظهر في كل جزء من الرسم واذا كانت بعض النقاط تظهر على خط الوسط الحسابي فتُحسب لصالح احد الجزئين المتجاورين ولا تُحسب مرتين.
8. نجمع نقاط الجزئين 2 + 4 ونرمز للمجموع بالحرف a، ونجمع نقاط الجزئين 1+3 و نرمز لهما بالحرف b.
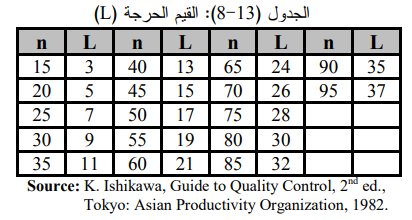
9 . مراجعة جدول القيم الحرجة (L) لتحديد القيمة الحرجة للعينة.
10. اجراء الاختبار الآتي :
أ ـ إذا كان a و b أصغر من L فان هناك علاقة قوية بين المتغيرين.
ب ـ إذا كان a و b أكبر من L فان ذلك يعني عدم وجود علاقة قوية بين المتغيرين .
ج ـ إذا كان a أصغر من L و b اكبر من L فان هناك علاقة موجبة بين المتغيرين.
د ـ إذا كان b أصغر من L و a اكبر من L فان هناك علاقة سالبة بين المتغيرين .
هـ ـ اذا كان a و b متساويين واكبر من L فذلك دليل على عدم وجود علاقة بين المتغيرين
ولتوضيح مخطط التبعثر سنستخدم المثال 13- 4
مثال 13- 4 :
في احد معامل الصناعات المعدنية تم سحب 20 قطعة مسطحة من الستيل لدراسة العلاقة بين عُرض القطعة وطولها ، اذ أُعيدت عدة صفائح مرفوضة من قبل الزبائن بسبب اختلاف عرض وطول القطعة المعدنية عن المواصفات . والجدول التالي يوضح قياسـات القطع المعدنية المسحوبة :
المطلوب : اعداد مخطط التبعثر وتحديد نوع العلاقة بين المتغيرين ان وجدت .
الحل :
بتطبيق الخطوة 7 وبجمع النقاط في كل جز نحصل على ما يلي :
الجزء 1 = 3 نقطة ، الجزء 2 = 7 نقاط
الجزء 3 = 4 نقاط ، الجزء 4 = 6 نقاط
الخطوة الثامنة نحسب قيمة a و b كالآتي :
a = 7 +6 = 13 b = 3 + 4 = 7
الخطوة التاسعة ، بما أن حجم العينة يساوي 20 فأن قيمة L من جدول القيم الحرجة (13-8) تساوي 5 .
الخطوة العاشرة ، أجراء الاختبار: لما كان a و b اكبر من L فنستـدل الى عدم وجود علاقة قوية بين المتغيرين (قاعدة 10- ب). مما تقدم نتوصل الى استنتاج مفاده عدم وجود علاقة قوية بين المتغيرين وهذا يدعو الى البحث عن سبب اخر وقد يكون من المجدي هنا استخدام مخطط السبب والأثر للوصول الى مسببات المعيب.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|