


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2019
Date: 8-3-2017
Date: 4-3-2019
|
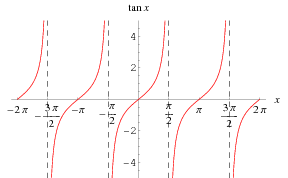
The tangent function is defined by
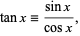 |
(1) |
where 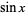 is the sine function and
is the sine function and 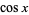 is the cosine function. The notation
is the cosine function. The notation 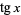 is sometimes also used (Gradshteyn and Ryzhik 2000, p. xxix).
is sometimes also used (Gradshteyn and Ryzhik 2000, p. xxix).

The common schoolbook definition of the tangent of an angle 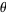 in a right triangle (which is equivalent to the definition just given) is as the ratio of the side lengths opposite to the angle and adjacent the angle, i.e.,
in a right triangle (which is equivalent to the definition just given) is as the ratio of the side lengths opposite to the angle and adjacent the angle, i.e.,
 |
(2) |
A convenient mnemonic for remembering the definition of the sine, cosine, and tangent is SOHCAHTOA (sine equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, tangent equals opposite over adjacent).
The word "tangent" also has an important related meaning as a line or plane which touches a given curve or solid at a single point. These geometrical objects are then called a tangent line or tangent plane, respectively.
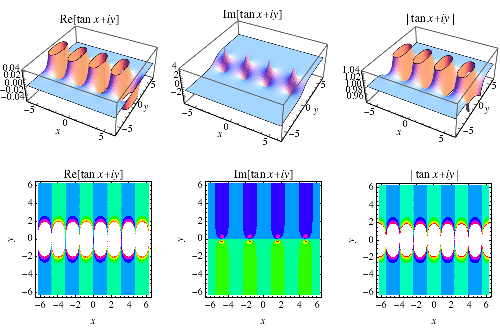 |
The definition of the tangent function can be extended to complex arguments 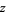 using the definition
using the definition
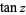 |
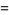 |
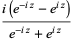 |
(3) |
 |
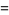 |
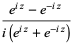 |
(4) |
 |
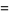 |
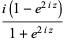 |
(5) |
 |
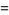 |
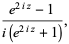 |
(6) |
where e is the base of the natural logarithm and i is the imaginary number. The tangent is implemented in the Wolfram Language as Tan[z].
A related function known as the hyperbolic tangent is similarly defined,
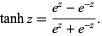 |
(7) |
An important tangent identity is given by
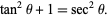 |
(8) |
Angle addition, subtraction, half-angle, and multiple-angle formulas are given by
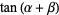 |
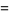 |
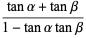 |
(9) |
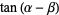 |
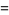 |
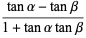 |
(10) |
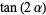 |
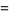 |
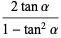 |
(11) |
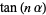 |
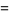 |
![(tan[(n-1)alpha]+tanalpha)/(1-tan[(n-1)alpha]tanalpha)](http://mathworld.wolfram.com/images/equations/Tangent/Inline29.gif) |
(12) |
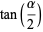 |
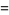 |
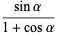 |
(13) |
 |
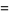 |
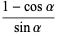 |
(14) |
 |
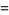 |
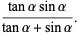 |
(15) |
The sine and cosine functions can conveniently be expressed in terms of a tangent as
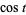 |
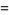 |
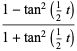 |
(16) |
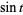 |
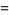 |
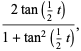 |
(17) |
which can be particularly convenient in polynomial computations such as Gröbner basis since it reduces the number of equations compared with explicit inclusion of 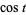 and
and 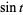 together with the additional relation
together with the additional relation 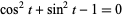 (Trott 2006, p. 39).
(Trott 2006, p. 39).
These lead to the pretty identity
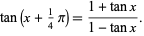 |
(18) |
There is also a beautiful angle addition identity for three variables,
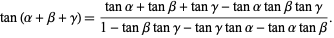 |
(19) |
Another tangent identity is
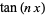 |
 |
 |
(20) |
 |
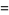 |
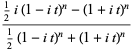 |
(21) |
 |
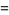 |
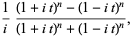 |
(22) |
where 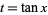 (Beeler et al. 1972). Written explicitly,
(Beeler et al. 1972). Written explicitly,
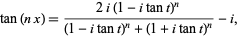 |
(23) |
This gives the first few expansions as
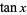 |
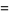 |
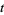 |
(24) |
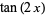 |
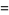 |
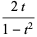 |
(25) |
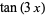 |
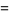 |
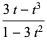 |
(26) |
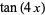 |
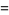 |
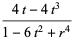 |
(27) |
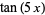 |
 |
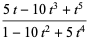 |
(28) |
(OEIS A034867 and A034839).
A beautiful formula that generalizes the tangent angle addition formula, (27), and (28) is given by
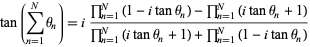 |
(29) |
(Szmulowicz 2005).
There are a number of simple but interesting tangent identities based on those given above, including
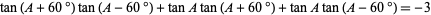 |
(30) |
(Borchardt and Perrott 1930).
The Maclaurin series valid for 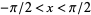 for the tangent function is
for the tangent function is
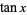 |
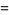 |
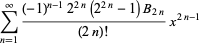 |
(31) |
 |
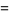 |
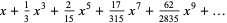 |
(32) |
(OEIS A002430 and A036279), where 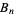 is a Bernoulli number.
is a Bernoulli number.
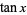 is irrational for any rational
is irrational for any rational 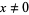 , which can be proved by writing
, which can be proved by writing 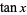 as a continued fraction as
as a continued fraction as
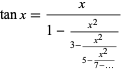 |
(33) |
(Wall 1948, p. 349; Olds 1963, p. 138) and
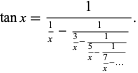 |
(34) |
both due to Lambert.
An interesting identity involving the product of tangents is
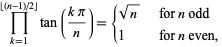 |
(35) |
where 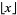 is the floor function.
is the floor function.
The equation
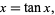 |
(36) |
which is equivalent to 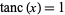 , where
, where 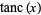 is the tanc function, does not have simple closed-form solutions.
is the tanc function, does not have simple closed-form solutions.
The difference between consecutive solutions gets closer and closer to 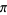 for higher order solutions. The function
for higher order solutions. The function 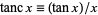 is sometimes known as the tanc function.
is sometimes known as the tanc function.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.
Beeler, M. et al. Item 16 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 9, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/recurrence.html#item16.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 226, 1987.
Borchardt, W. G. and Perrott, A. D. Ex. 33 in A New Trigonometry for Schools. London: G. Bell, 1930.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Sloane, N. J. A. Sequences A002430/M2100, A034839, A034867, A036279, and A115365 in "The On-Line Encyclopedia of Integer Sequences."
Szmulowicz, F. "New Analytic and Computational Formalism for the Band Structure of  -Layer Photonic Crystals." Phys. Lett. A345, 469-477, 2005.
-Layer Photonic Crystals." Phys. Lett. A345, 469-477, 2005.
Spanier, J. and Oldham, K. B. "The Tangent  and Cotangent
and Cotangent  Functions." Ch. 34 in An Atlas of Functions.Washington, DC: Hemisphere, pp. 319-330, 1987.
Functions." Ch. 34 in An Atlas of Functions.Washington, DC: Hemisphere, pp. 319-330, 1987.
Tropfke, J. Teil IB, §2. "Die Begriffe von Tangens und Kotangens eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 23-28, 1923.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.



|
|
|
|
هذه العلامة.. دليل على أخطر الأمراض النفسية
|
|
|
|
|
|
|
بالفيديو: بعثة الإغاثة الطبية التابعة للعتبة الحسينية في لبنان تقدم لاهالي صيدا المساعدات الطبية
|
|
|