


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 29-8-2016
Date: 3-9-2016
Date: 2-8-2016
|
Hot Box and Particle Creation
The electromagnetic radiation in a box of volume V can be treated as a noninteracting ideal Bose gas of photons. If the cavity also contains atoms capable of absorbing and emitting photons, the number of photons in the cavity is not definite. The box is composed of a special material that can withstand extremely high temperatures of order τ >> τe = me c2.
a) Derive the average number of photons in the box.
Hint:
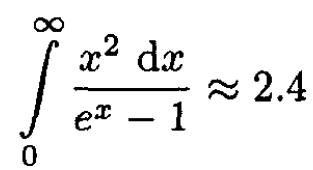
b) What is the total energy of the radiation in the box for τ/τe << 1?
c) What is the entropy of the radiation for τ/τe << 1?
d) Assume that photons can create neutral particles of mass m and zero spin and that these neutral particles χ can create photons by annihilation or some other mechanism. The cavity now contains photons and particles in thermal equilibrium at a temperature τ. Find the particle density n = N/V. Consider only the process where a single photon is emitted or absorbed by making a single particle.
Hint: Minimize the free energy.
Now, instead of neutral particles, consider the creation of electron-positron pairs.
e) What is the total concentration of electrons and positrons inside the box when τ/τe << 1?
f) What is the total concentration of electrons and positrons when τ/τe >> 1?
Hint:
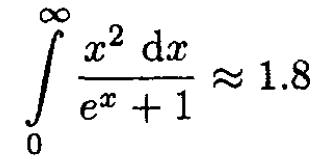
SOLUTION
a) The number of photons is
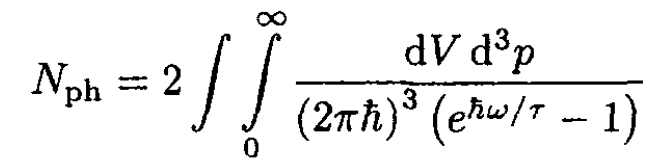 (1)
(1)
where the factor 2 comes from the two polarizations of photons; p = hk = hω/c. So,
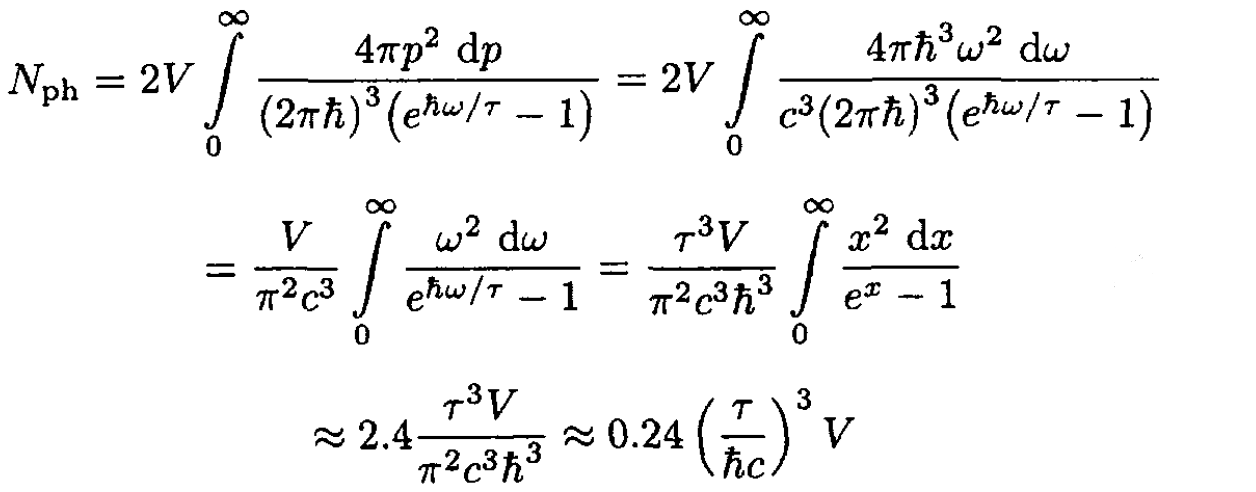 (2)
(2)
b) At low temperatures we can disregard any interaction between photons due to the creation of electron–positron pairs. We can therefore use the standard formula for energy flux:
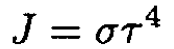 (3)
(3)
where σ is the Stefan–Boltzmann constant. On the other hand, by analogy with molecular flow,
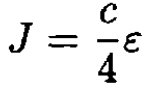 (4)
(4)
where ε = E/V is the energy density. So,
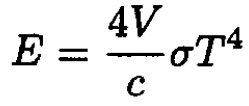 (5)
(5)
c) Using the equation of state for a photon gas
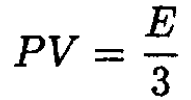 (6)
(6)
and
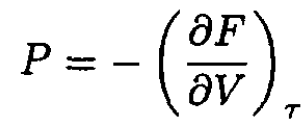 (7)
(7)
we have
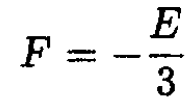 (8)
(8)
The entropy S is then
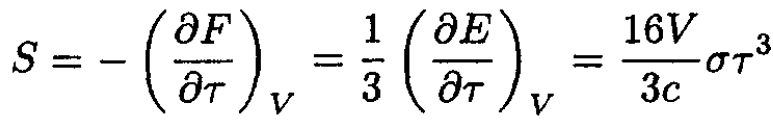 (9)
(9)
d) The energy E of the system of particles + photons is
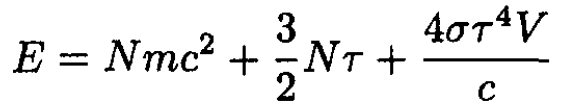 (10)
(10)
The entropy of the system is the sum of the entropy of an ideal gas and radiation. The free energy of a single-particle ideal gas with s = 0 of created particles and the radiation is then
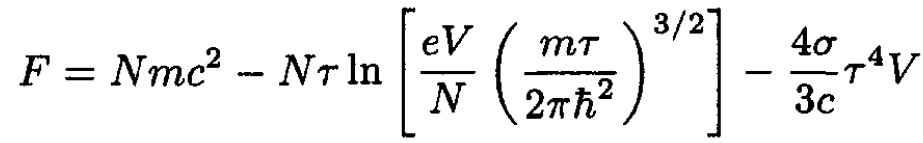 (11)
(11)
Minimizing the free energy with respect to the number of particles, we have
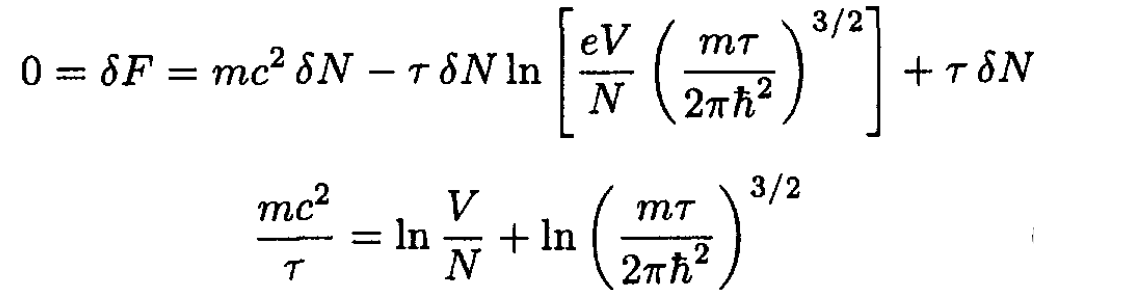 (12)
(12)
From (12) we obtain
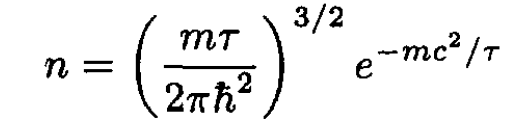 (13)
(13)
This result can be immediately obtained if we consider the process as a “chemical” reaction
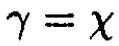
or
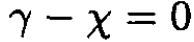
For chemical equilibrium
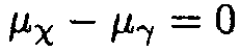
Since, for photons, μ = 0, we have
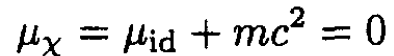
where μid is the chemical potential of an ideal gas (see part (e)). This result gives us (13).
e) Pair creation and annihilation can be written in the form
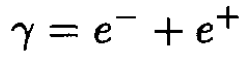 (14)
(14)
The chemical potential μ of the photon gas is zero (since the number of photons is not constant but is defined by equilibrium conditions). Therefore, we have for process (14) in equilibrium:
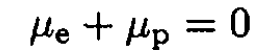 (15)
(15)
where μe and μp are the chemical potentials of electrons and positrons, respectively. If we disregard the walls of the box and assume that there are no electrons inside the box initially, then the number of electrons equals the number of positrons, and μe = μp = 0 We then find for the number of electrons (positrons)
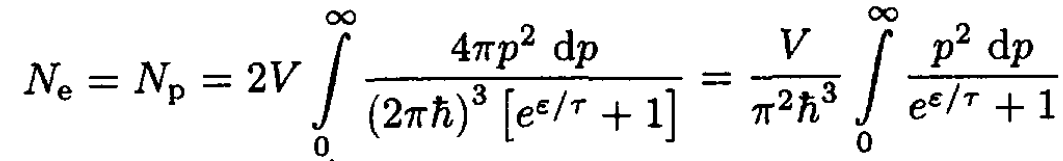 (16)
(16)
where the factor 2 comes from the double degeneracy of the electron gas g = 2s + 1, and we set μ = 0. The energy may be written
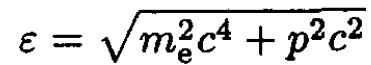
Disregarding the 1 in the denominator of (16) and expanding the square root with respect to the small parameter p2/m2ec2, for τ << mec2 we obtain, from (16),
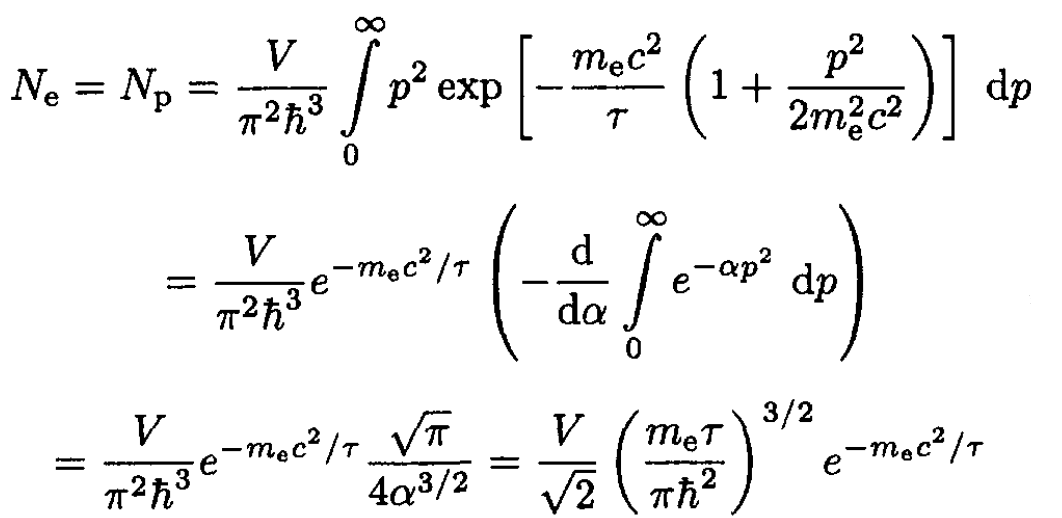 (17)
(17)
where we set α ≡ 1/2meτ. We then find that the concentrations are
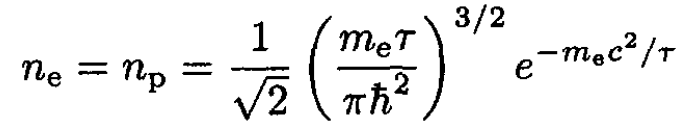 (18)
(18)
and so
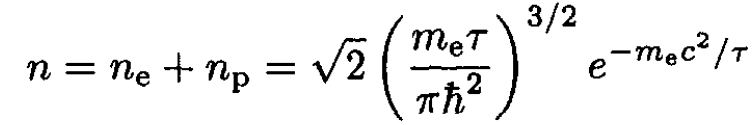 (19)
(19)
Alternatively, we can take an approach similar to the one in (d). Using the formula for the chemical potential of an ideal gas gives
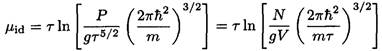 (20)
(20)
We can immediately write
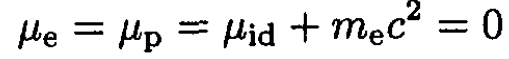
to obtain the same result in (18) and (19).
f) For τ >> mec2 the electrons are highly relativistic, and we can write ε = cp in (16). Then
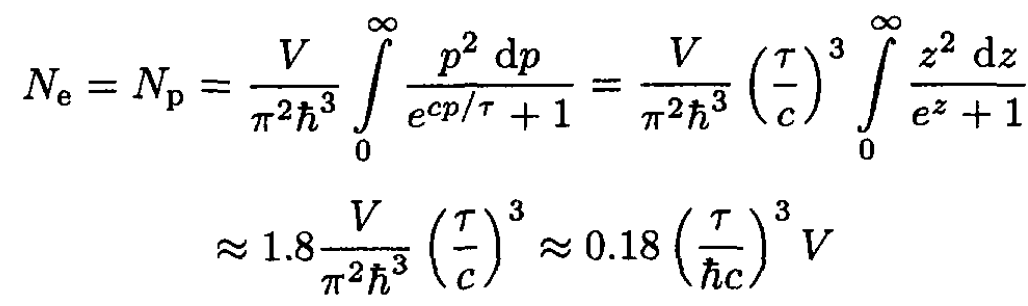 (21)
(21)
where we have used the integral given in the problem. Finally,
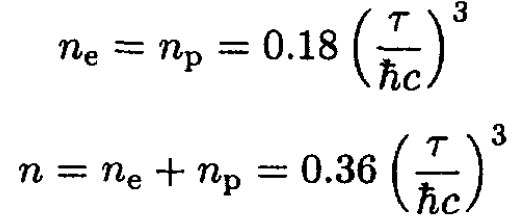 (22)
(22)



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|