Unwinding String

A point mass m is attached to a long, massless thin cord whose other end is attached to a fixed cylinder of radius R. Initially, the cord is snugly and completely wound up around a circular cross section of the cylinder, so that the mass touches the cylinder. No external forces are acting, except for an impulse at t = 0 directed radially outward to give the mass m an initial velocity of magnitude v₀. This starts the mass unwinding (see Figure 1.1a). The point P is the initial position of the mass, and Q denotes the instantaneous contact point between the cord and the cylinder.

Figure 1.1a

a) Find the Lagrangian and equation of motion in terms of the generalized coordinate θ as a function of time, satisfying the initial conditions.

b) Using the above solution, find the angular momentum of the mass about the center of the cylinder. Is angular momentum conserved? Why? Is the energy conserved? Why?

c) Now consider a new situation in which the cylinder, taken to be hollow and of mass M (same radius R), can spin freely as the mass unwinds. The new angle φ measures the position of P (the place where the mass was at rest) with respect to the vertical axis (see Figure 1.1b). Write down the Lagrangian in terms of the generalized

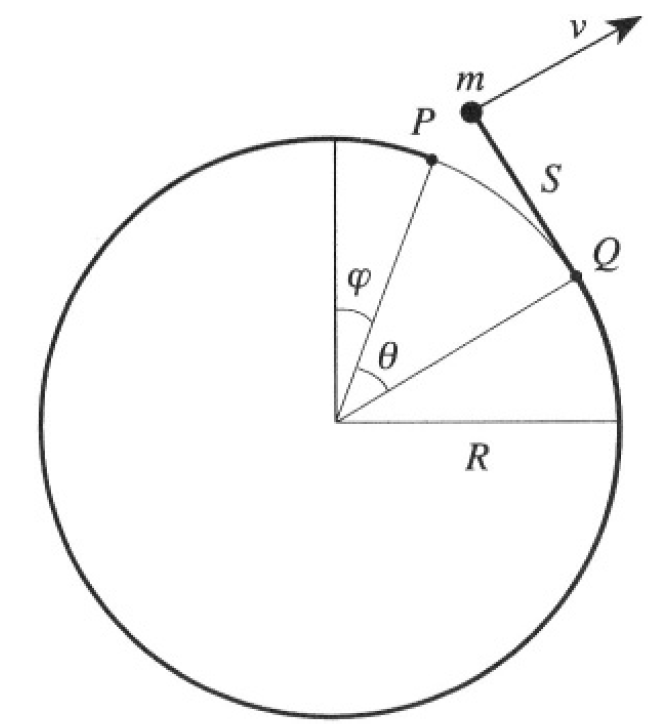
Figure 1.1b

 coordinates θ and φ. Identify two conserved quantities and express them as functions of θ and φ.

d) Solve for θ(t). Which way does the cylinder spin?

SOLUTION

a) You can write a Lagrangian using Cartesian coordinates x, y and express it as a function of 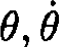 (see Figure 1.2a). However, if you notice that the length of the unwound string Rθ, is and it unwinds with angular velocity  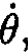you can immediately write a Lagrangian, which is just a kinetic energy in this case

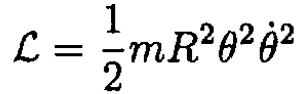
The equation of motion will be

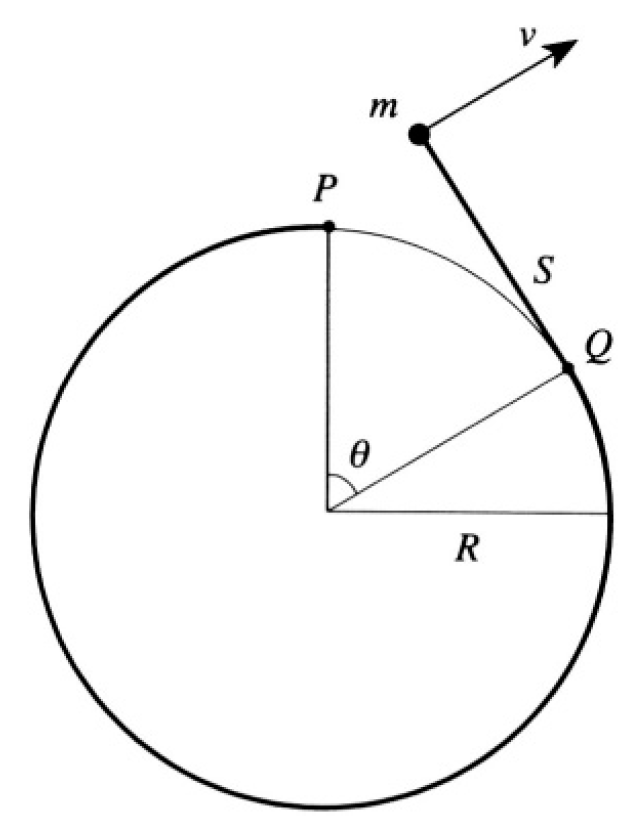
Figure 1.2a

or

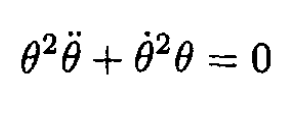
or for θ ≠ 0,

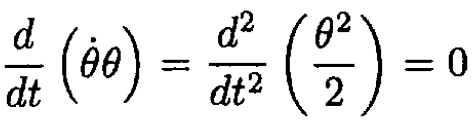
whose solution is θ² = 2At + B. From the initial condition θ(0) = 0 and

i.e., 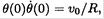  we conclude that B = 0 and A = v₀/R, so

b) The angular momentum 1 about the center of the cylinder is given by

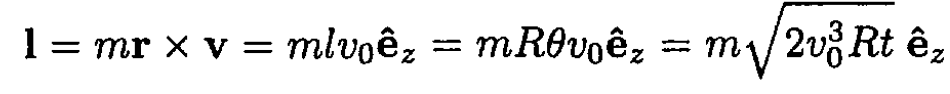
The angular momentum is not conserved, since there is a torque from the cord connected to the cylinder; the energy, on the other hand, is conserved, because the force on the mass m is always perpendicular to its velocity:

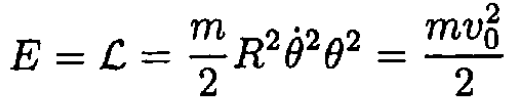
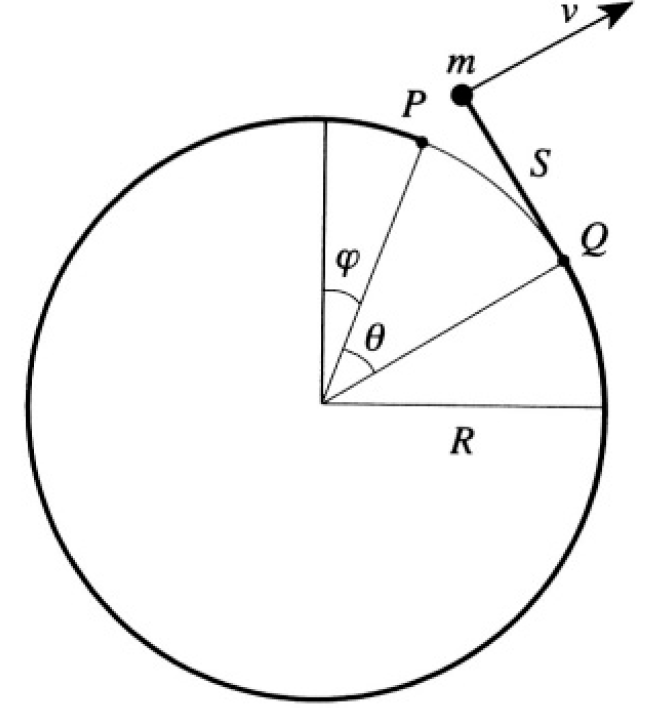
Figure 1.2b

c) Again we can employ cartesian coordinates (see Figure 1.2b), but if we use the fact that the cord is always perpendicular to the radius of the cylinder at the point of contact we can write the Lagrangian in the form

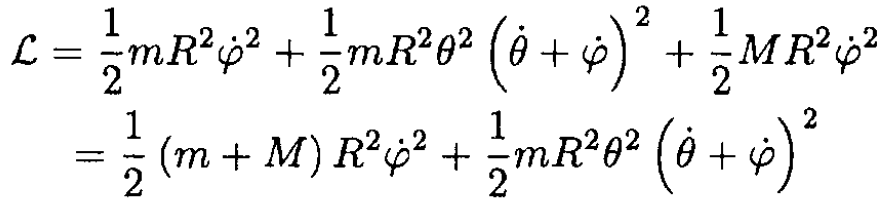
From this equation, we can immediately obtain the integrals of motion. An angular momentum which is now conserved is

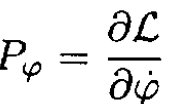(1)

Initially, it is equal to zero, and since the initial impulse does not give the system any angular momentum, it will be zero for all time. So, we have from (1)

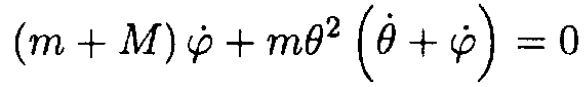(2)

The energy is also conserved:

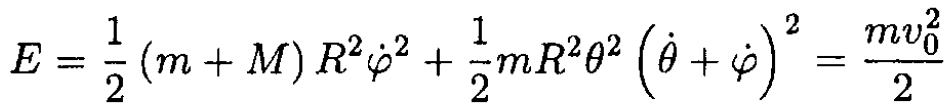(3)

d) From equation (2) we can express 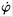 in terms of θ and :

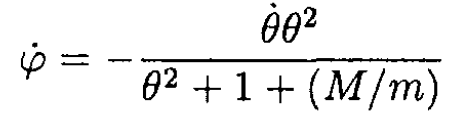(4)

Substituting (4) into (3) we obtain

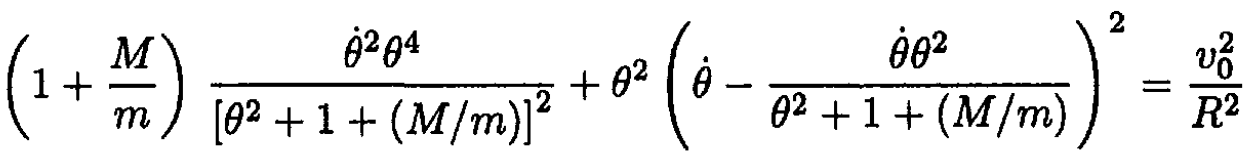
After some algebra, letting α ≡ 1 + (M/m) and β ≡ (v²₀/R²) we have

Integrating this equation results in

Therefore:

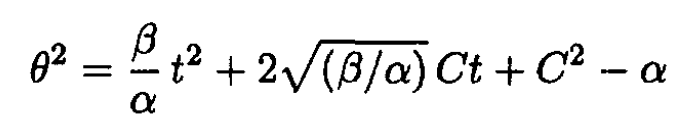
From the initial condition θ(0) = 0, we find that C² = α, so

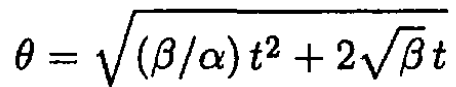
Substituting back α and β we have

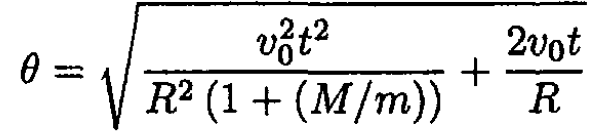
For M/m = → ∞ (i.e., a fixed cylinder), this result reduces to that obtained in (a). It is obvious from angular momentum conservation that the cylinder would spin in the opposite direction from that of the unwinding cord. Indeed, from (4) we see that if 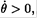 then