According to the variation of parameters formula, the solution of (ODE) for a given control α(.) is

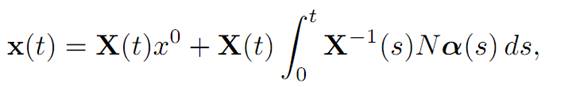
where X(t) = e^tM. Furthermore, observe that

                          x⁰∈ C(t)

if and only if  (1.1) there exists a control α(.) ∈ A such that x(t) = 0 if and only if

(1.2)

If and only if

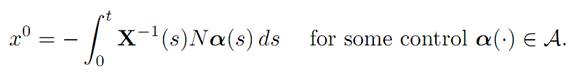(1.3)

We make use of these formulas to study the reachable set:

THEOREM 1.2 (STRUCTURE OF REACHABLE SET).

(i) The reachable set C is symmetric and convex.

(ii) Also, if x0 ∈ C(t¯), then x⁰ ∈ C(t) for all times t ≥  t^-.

DEFINITIONS.

(i) We say a set S is symmetric if x ∈ S implies −x ∈ S.

(ii) The set S is convex if x, xˆ ∈ S and 0 ≤ λ ≤ 1 imply λx + (1 − λ) xˆ ∈ S.

Proof. 1. (Symmetry) Let t ≥ 0 and x⁰ ∈ C(t). Then

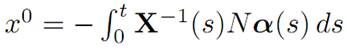
for some admissible control α ∈ A. Therefore

−α ∈ A since the set A is symmetric. Therefore −x⁰ ∈ C(t), and so each set C(t)  symmetric. It follows that C is symmetric.

2. (Convexity) Take

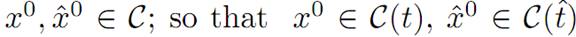
for appropriate times t, tˆ ≥ 0. Assume t ≤ tˆ. Then

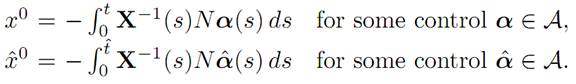
Define a new control

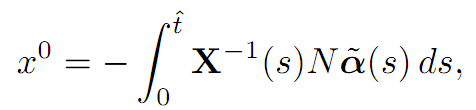
and hence x⁰ ∈ C(tˆ). Now let 0 ≤ λ ≤ 1, and observe

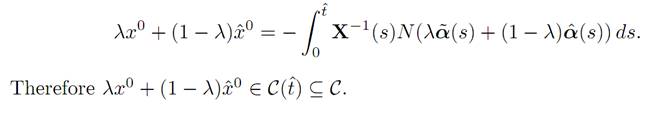
3. Assertion (ii) follows from the foregoing if we take  t¯= tˆ.

A SIMPLE EXAMPLE. Let n = 2 and m = 1, A = [−1, 1], and write x(t) = (x¹(t), x²(t))^T . Suppose

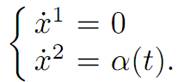
This is a system of the form x˙ = Mx + Nα, for

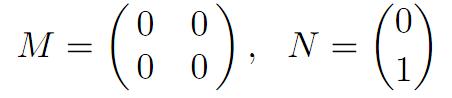
Clearly C = {(x¹, x²⁾ | x¹ = 0}, the x²–axis.

We next wish to establish some general algebraic conditions ensuring that C contains a neighborhood of the origin.

DEFINITION. The controllability matrix is

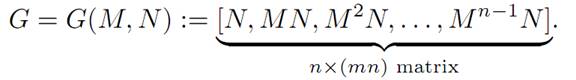
THEOREM 1.3 (CONTROLLABILITY MATRIX). We have

                              Rank G = n

 and only if

                                              0 ∈ C◦.

NOTATION. We write C◦ for the interior of the set C. Remember that

rank of  G = number of linearly independent rows of G

                    = number of linearly independent columns of G.

Clearly rank G ≤ n.

Proof. 1. Suppose first that rank G < n. This means that the linear span of the columns of G has dimension less than or equal to n − 1. Thus there exists a vector b ∈ Rⁿ, b = 0, orthogonal to each column of G. This implies

                                   b^TG = 0

and so

           b^TN = b^TMN =  …..  = b^TMⁿ⁻¹N = 0.

2. We claim next that in fact

(1.4)                    b^TM^kN = 0 for all positive integers k.

To confirm this, recall that

                                    p(λ) := det(λI −M)

is the characteristic polynomial of M. The Cayley–Hamilton Theorem states that

                                        p(M) = 0.

So if we write

Similarly,

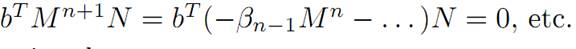
The claim (1.4) is proved.

Now notice that

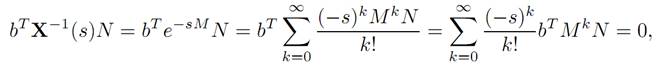
according to (1.4).

3. Assume next that x⁰ ∈ C(t). This is equivalent to having

This says that b is orthogonal x⁰ . In other words, C must lie in the hyperplane orthogonal to b ≠ 0. Consequently C^◦ = ∅.

4. Conversely, assume 0 ∉C^◦. Thus 0 ∉C^◦(t) for all t > 0. Since C(t) is convex, there exists a supporting hyperplane to C(t) through 0. This means that there exists b = 0 such that b. x⁰ ≤ 0 for all x⁰ ∈ C(t).

Choose any x⁰ ∈ C(t). Then

for some control α, and therefore

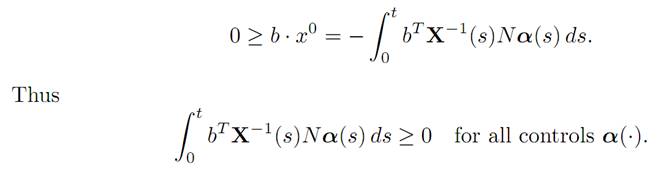
We assert that therefore

(1.5)                                                    b^TX⁻¹ (s)N ≡ 0,

a proof of which follows as a lemma below. We rewrite (2.5) as

(1.6)                                                   b^T e^−sMN ≡ 0.

Let s = 0 to see that b^TN = 0. Next differentiate (1.6) with respect to s, to find that

                                                  b^T (−M)e^−sMN ≡ 0.

For s = 0 this says

                                                  b^TMN = 0.

We repeatedly differentiate, to deduce

b^TM^kN = 0 for all k = 0, 1, . . . ,

and so b^TG = 0. This implies rank G < n, since b = 0.

LEMMA 1.4 (INTEGRAL INEQUALITIES). Assume that

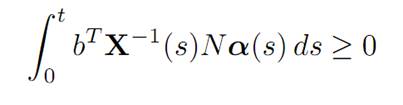(1.7)

for all α(.) ∈ A. Then

                             b^TX⁻¹ (s)N ≡ 0.

Proof. Replacing α by −α in (1.7), we see that

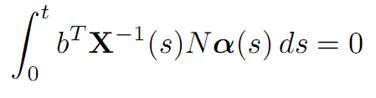
for all α(.) ∈ A. Define

v(s) := b^TX⁻¹ (s)N.

If v /≡ 0, then v(s₀)≠0 for some s₀. Then there exists an interval I such that s₀ ∈ I and v = 0 on I. Now define α(.) ∈ A this way:

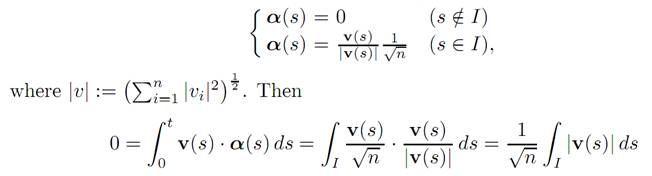
This implies the contradiction that v ≡ 0 in I.

DEFINITION. We say the linear system (ODE) is controllable if C = Rⁿ.

THEOREM 1.5 (CRITERION FOR CONTROLLABILITY). Let A be the cube [−1, 1] ⁿ in Rⁿ. Suppose as well that rank G = n, and Re λ < 0 for each

eigenvalue λ of the matrix M.

Then the system (ODE) is controllable.

Proof. Since rank G = n, Theorem 1.3 tells us that C contains some ball B centered at 0. Now take any x⁰ ∈ Rⁿ and consider the evolution

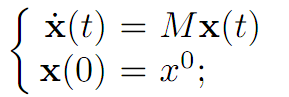
in other words, take the control α(.) ≡ 0. Since Re λ < 0 for each eigenvalue λ of M, then the origin is asymptotically stable. So there exists a time T such that x(T) ∈ B. Thus x(T) ∈ B ⊂ C; and hence there exists a control α(.) ∈ A steering x(T) into 0 in finite time.

EXAMPLE. We once again consider the rocket railroad car, from §1.2, for which n = 2, m = 1, A = [−1, 1], and

Therefore

rank G = 2 = n.

Also, the characteristic polynomial of the matrix M is

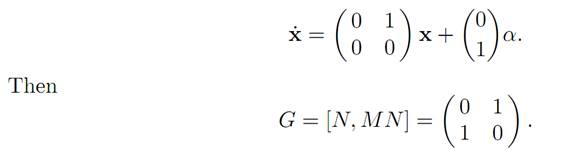
Since the eigenvalues are both 0, we fail to satisfy the hypotheses of Theorem 1.5.

This example motivates the following extension of the previous theorem:

THEOREM 1.6 (IMPROVED CRITERION FOR CONTROLLABILITY). Assume rank G = n and Re λ ≤ 0 for each eigenvalue λ of M.

Then the system (ODE) is controllable.

Proof. 1. If C≠ Rⁿ, then the convexity of C implies that there exist a vector b ≠0 and a real number μ such that

(1.8)                                        b .x⁰≤ μ

for all x⁰ ∈ C. Indeed, in the picture we see that  b .(x⁰ − z⁰) ≤ 0; and this implies   (1.8) for μ := b . z⁰.

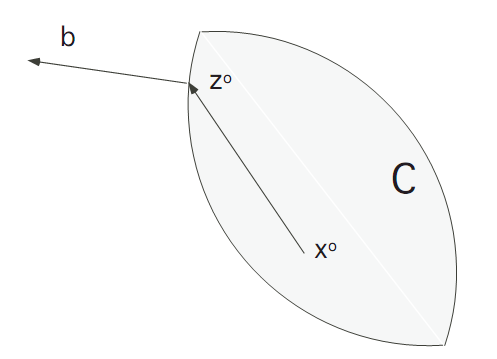
We will derive a contradiction.

2. Given b≠0,μ∈ R, our intention is to find x⁰ ∈ C so that (1.8) fails. Recall x⁰ ∈ C if and only if there exist a time t > 0 and a control α(.) ∈ A such that

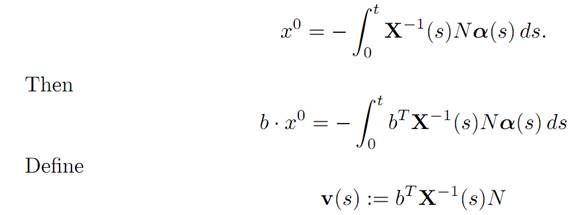
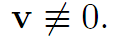(1.9)

To see this, suppose instead that v ≡ 0. Then k times differentiate the expression b^TX⁻¹(s)N with respect to s and set s = 0, to discover

                                         b^TM^kN = 0

for k = 0, 1, 2, . . . . This implies b is orthogonal to the columns of G, and so rank G < n. This is a contradiction to our hypothesis, and therefore (1.9) holds.

4. Next, define α(.) this way:

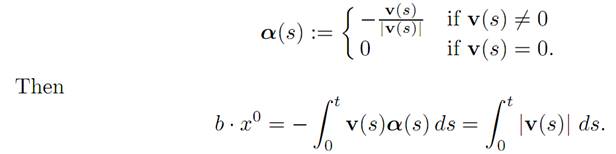
We want to find a time t > 0 so that

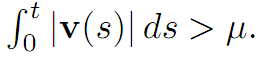
In fact, we assert that

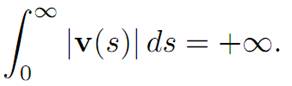(1.10)

To begin the proof of (1.10), introduce the function

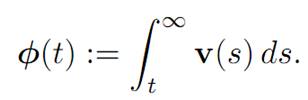
We will find an ODE φ satisfies. Take p(.) to be the characteristic polynomial of M. Then

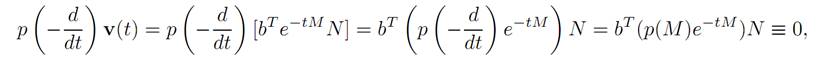
since p(M) = 0, according to the Cayley–Hamilton Theorem. But since p (− d/dt) v(t) ≡0, it follows that

Hence φ solves the (n + 1)^th order ODE

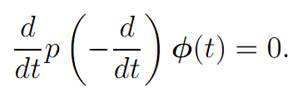
We also knowLet μ₁, . . . ,μ _n+1 be the solutions of μ p(−μ) = 0. According to ODE theory, we can write

                        φ(t) = sum of terms of the form pi(t)e^{μ​ it}

for appropriate polynomials pi(.).

Furthermore, we see that μ_n+1 = 0 and μ_k = −λ_k, where λ₁, . . . , λ_n are the eigenvalues of M. By assumption Re μ_k ≥ 0, for k = 1, . . . , n. If

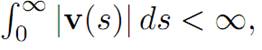
Then

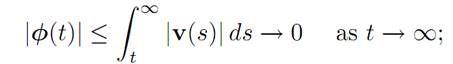
that is, φ(t) → 0 as t → ∞. This is a contradiction to the representation formula of φ(t) = Σpi(t)e^μit, with Re μ_i ≥ 0. Assertion (1.10) is proved.

5. Consequently given any μ, there exists t > 0 such that

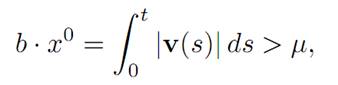
a contradiction to (1.8). Therefore C = Rⁿ.

References

[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.

[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.

[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.

[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.

[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.

[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.

[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.

[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.

[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.

[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).

[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.

[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.

[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.

[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.

[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.

[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.

[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.

[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.

[T] William J. Terrell, Some fundamental control theory I: Controllability, observability,  and duality, American Math Monthly 106 (1999), 705–719.

مواضيع ذات صلة

DYNAMIC PROGRAMMING-DYNAMIC PROGRAMMING AND THE PONTRYAGIN MAXIMUM PRINCIPLE

DYNAMIC PROGRAMMING-EXAMPLES

DERIVATION OF BELLMAN,S PDE-DYNAMIC PROGRAMMING

THE PONTRYAGIN MAXIMUM PRINCIPLE-MORE APPLICATIONS

THE PONTRYAGIN MAXIMUM PRINCIPLE-MAXIMUM PRINCIPLE WITH STATE CONSTRAINTS

THE PONTRYAGIN MAXIMUM PRINCIPLE-MORE APPLICATIONS

THE PONTRYAGIN MAXIMUM PRINCIPLE-MAXIMUMPRINCIPLEWITH TRANSVERSALITY CONDITIONS

THE PONTRYAGIN MAXIMUM PRINCIPLE-APPLICATIONS AND EXAMPLES

THE PONTRYAGIN MAXIMUM PRINCIPLE-STATEMENT OF PONTRYAGIN MAXIMUM PRINCIPLE

THE PONTRYAGIN MAXIMUM PRINCIPLE-REVIEW OF LAGRANGE MULTIPLIERS.

THE PONTRYAGIN MAXIMUM PRINCIPLE-CALCULUS OF VARIATIONS, HAMILTONIAN DYNAMICS

LINEAR TIME-OPTIMAL CONTROL-EXAMPLES