Principle of Conformal Mapping

a) Show that the real part U(x, y) and the imaginary part V(x, y) of a differentiable function W(z) of z = z + iy obey Laplace’s equation.

b) If U(x, y) and V(x, y) above are the potentials of two fields F and G in two dimensions, show that at each point (x, y), the fields F and G are orthogonal.

c) Consider the function W(z) = A ln z, where A is a real constant. Find the fields F and G and mention physical (Electrodynamics) problems in which they might occur.

SOLUTION

A differentiable function W(z) = U(x, y) + iV (x, y) satisfies the Cauchy Riemann conditions

(1)

To check that U and V satisfy Laplace’s equation, differentiate (1)

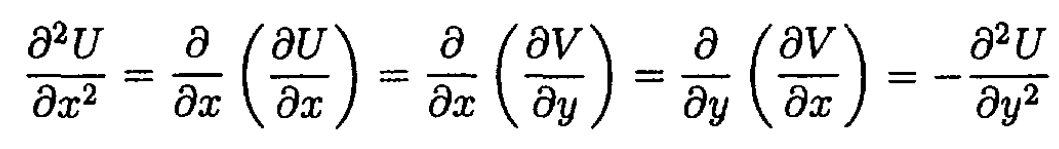
or

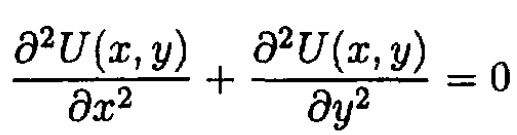
Similarly,

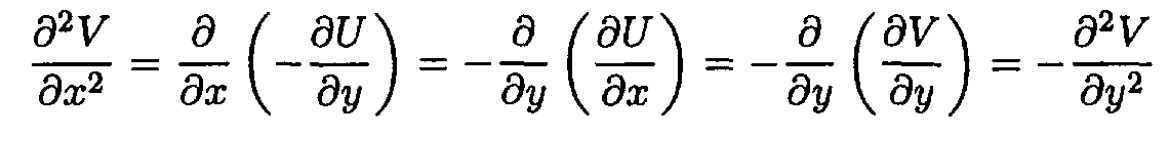
and

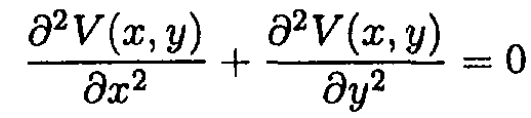
b) Orthogonality of the functions F and G also follows from (1):

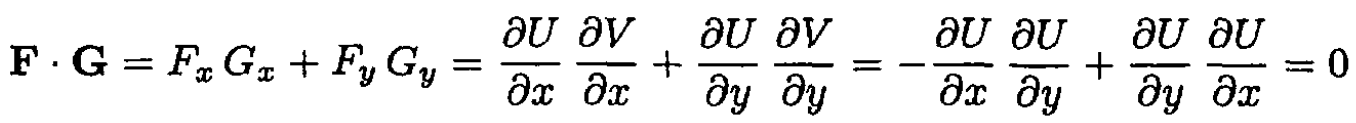
c) The electric field of an infinitely long charged wire passing through the origin is given by 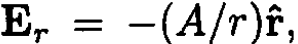 where A = -2λ and λ is the charge per unit length, r is the distance from the wire (see Figure 1.1). The complex potential

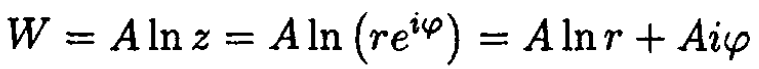
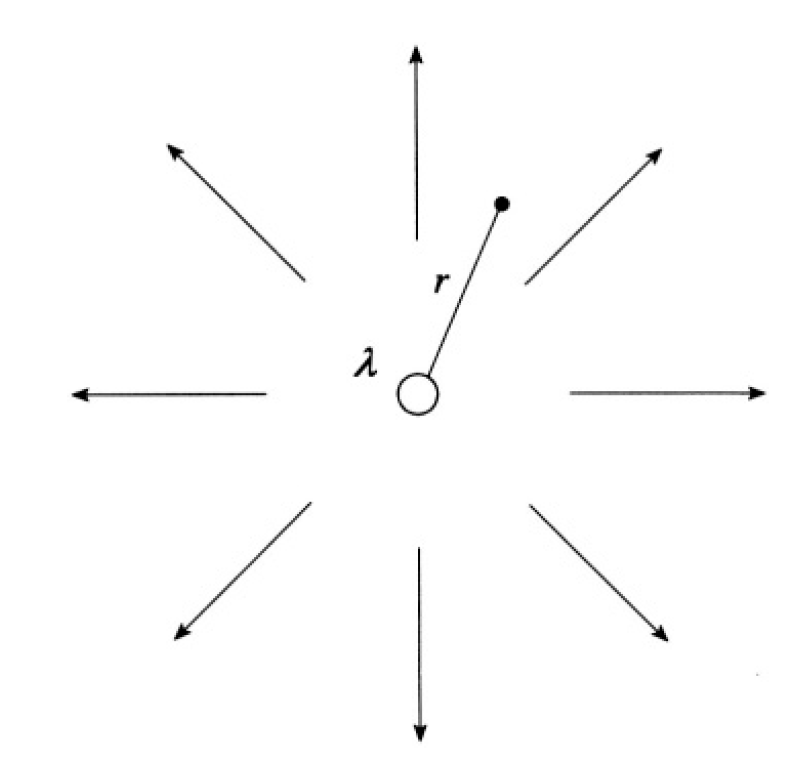
Figure 1.1

So

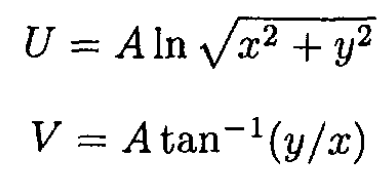
The fields F and G are given by

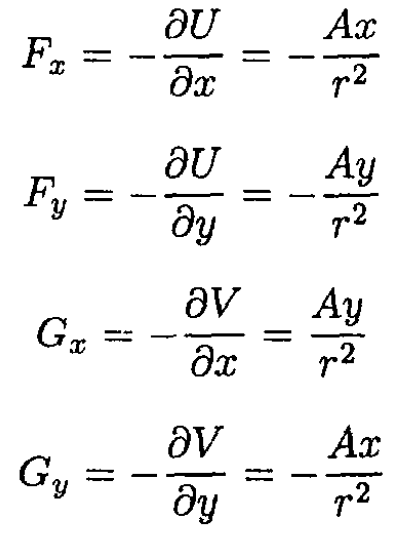
Note how F and G satisfy the conditions of parts (a) and (b). The magnetic field of a similarly infinite line current can be described by the same potential.