


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 25-8-2016
Date: 13-7-2016
Date: 22-8-2016
|
Superconducting Sphere in Magnetic Field
A superconducting (Type I) spherical shell of radius R is placed in a uniform magnetic field B0 (B0 << Hc, Hc, the critical field). Find
a) the magnetic field everywhere outside the shell
b) the surface current density
Hint: Inside, B = 0.
SOLUTION
a) Prom symmetry considerations, it is clear that the current would flow on the surface of the shell perpendicular to the applied magnetic field. As for any ellipsoid in a uniform electric or magnetic field, we can assume that the field outside the shell produced by these currents is equivalent to a magnetic dipole moment m placed in the center of the shell. For
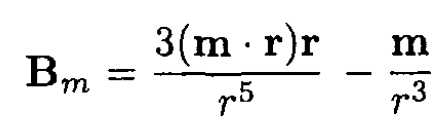
The total field outside is then B = Bm + B0. The boundary condition on the surface at an arbitrary point gives
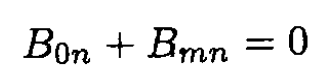
The normal component of B is continuous and inside B = 0. From the boundary conditions on the surface at an arbitrary angle θ between the direction of B0 and the normal n (see Figure 1.1) we have
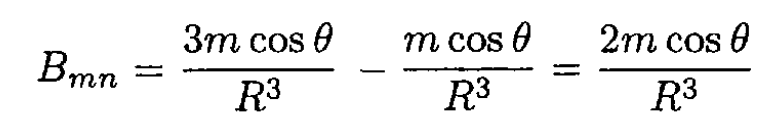 (1)
(1)
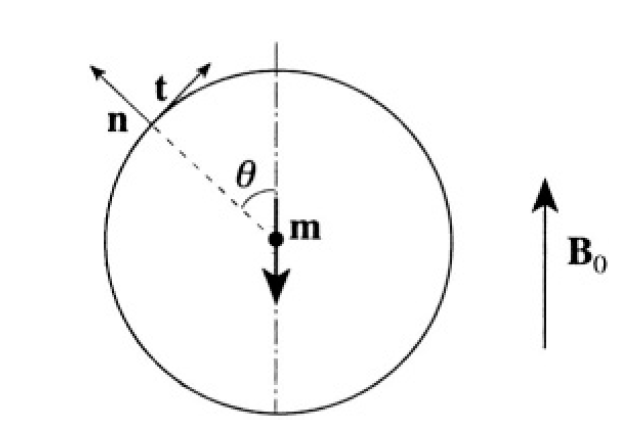
Figure 1.1
Hence
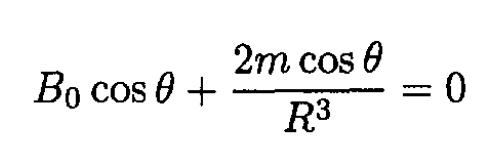 (2)
(2)
At m = -(R3/2) B0, where R is the radius of the spherical shell, the boundary conditions are satisfied on the surface of the shell. Therefore,
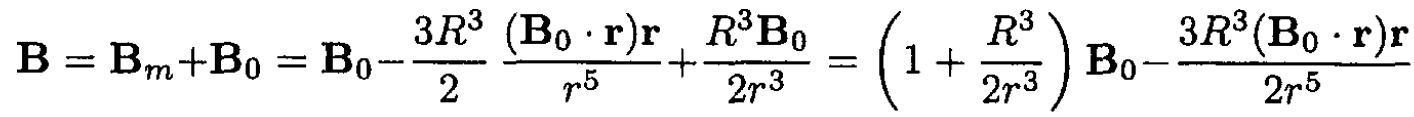
b) The surface current density Js can be found by using tangential H component continuity:
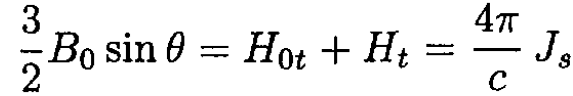
and therefore Js(θ) = 3cB0 sin θ/8π. This solution is only true while B < 2/3 Hc, and the whole sphere is superconducting. When B > 2/3 Hc the field at the equator exceeds Hc, and the sphere goes into an intermediate state.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|