Space Habitat Baseball

On Earth a baseball player can hit a ball 120 m by giving it an initial angle of 45° to the horizontal. Take the acceleration due to gravity as g = 10 m/s². Suppose the batter repeats this exercise in a space 'habitat' that has the form of a circular cylinder of radius R = 10 km and has an angular velocity about the axis of the cylinder sufficient to give an apparent gravity of g at radius R. The batter stands on the inner surface of the habitat (at radius R) and hits the ball in the same way as on Earth (i.e., at 45° to the surface), in a plane perpendicular to the axis of the cylinder (see Figure 1.1). What is the furthest distance the batter can hit the ball, as measured along the surface of the habitat?

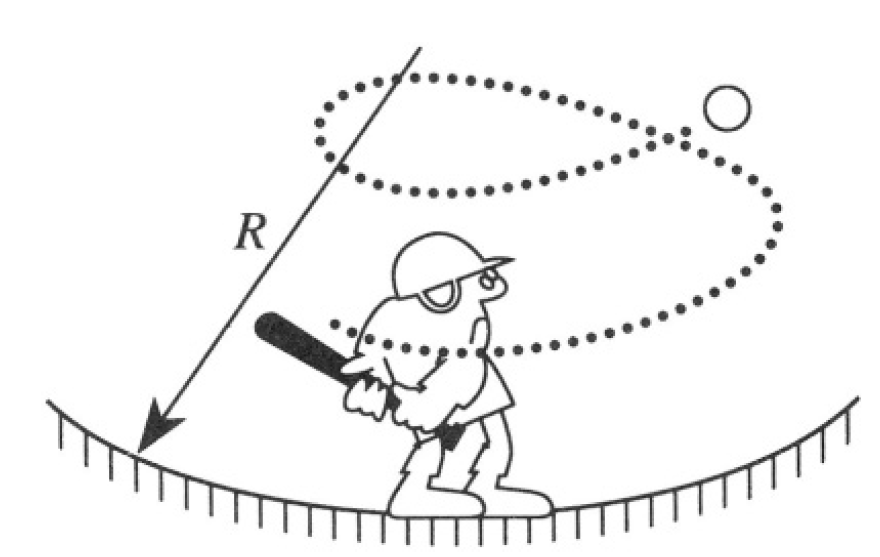
Figure 1.1

SOLUTION

On Earth, we can disregard the Coriolis force since it is only a second-order correction. If the player hits the ball with an initial velocity v, the maximum distance will be for the angle α = 45^o (neglecting also the effects of air resistance). Then, we calculate the range L by decomposing the trajectory into its component motions, with initial velocities v_x = v cos α, v_y = v sin α

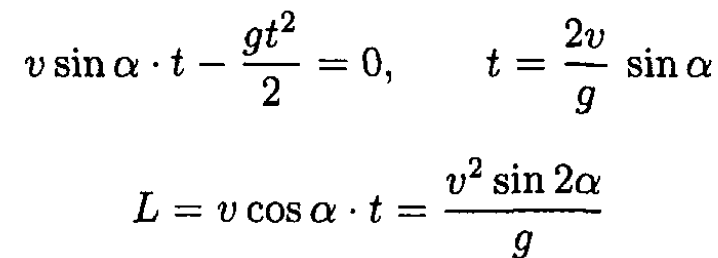
resulting in an initial velocity off the bat of

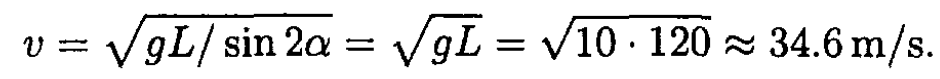(1)

On the surface of the habitat we can no longer disregard the Coriolis force (see Figure 1.2), so if we consider the problem in the rotating frame of the cylinder, the equations of motion become rather complicated. Therefore, let us view the exercise in the inertial frame. To provide the same apparent gravitational acceleration g, the cylinder has to rotate with an angular velocity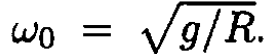 The instantaneous linear velocity of the point P where the player stands will be

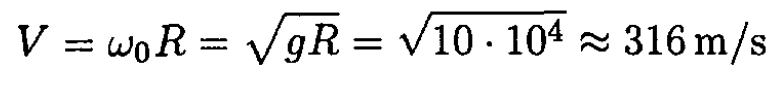(2)

Figure 1.2

When the ball leaves the surface, no forces act on it in the inertial frame. Its velocity is either u₊ or u_- where the velocities of the ball in the rotating frame v_x and the habitat V are parallel or antiparallel, respectively:

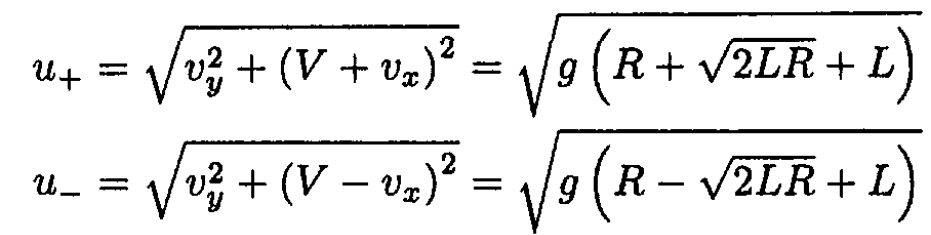(3)

The angle β of the line  of length D to the tangent of the circle is found using (1)–( 3):

The distance along the surface of the cylinder PO will then be s₁ = 2Rβ. During the time of the flight, the cylinder rotates by an angle θ_± = ω₀t_± = ω₀D/u_± and the distance s₂ will be

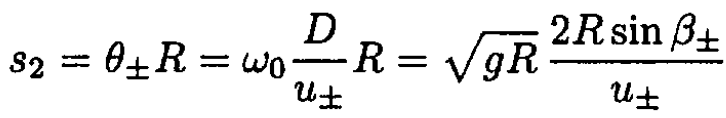(4)

The distance the player would hit the ball measured along the surface of the habitat is

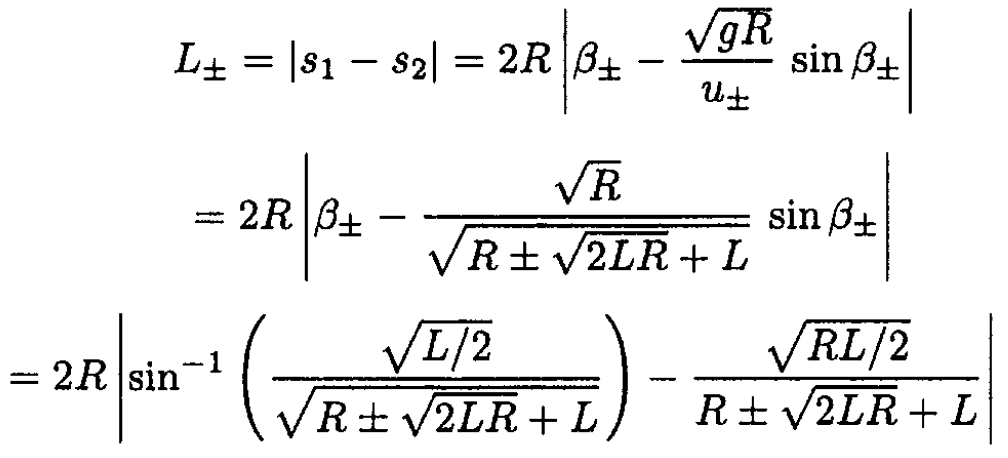(5)

Substituting numerical values into (5) we obtain

Therefore, to hit the furthest, the player should hit in the direction opposite to the direction of the habitat’s rotation.

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين