The classic diet problem is to organize a healthy diet and pay the lowest price for it. It was a prototype for problems in linear programming, a subject developed in the 1940s that is now used in a wide range of applications.

At the beginning of March Tanya takes a trip to the supermarket and checks out Solido and Liquex. On a back of a packet of Solido she finds out it contains 2 mg vitamins and 10 mg minerals, while a carton of Liquex contains 3 mg vitamins and 50 mg minerals. She dutifully fills her trolley with 30 packets of Solido and 5 cartons of Liquex to keep herself going for the month. As she proceeds towards the checkout she wonders if she has the right amount. First she calculates how many vitamins she has in the trolley. In the 30 packets of Solido she has 2 × 30 = 60 mg vitamins and in the Liquex, 3 × 5 = 15. Altogether she has 2 × 30 + 3 × 5 = 75 mg vitamins. Repeating the calculation for minerals, she has 10 × 30 + 50 × 5 = 550 mg minerals.

As the coach required her to have at least 120 mg vitamins and 880 mg minerals, she needs more packets and cartons in the trolley. Tanya’s problem is juggling the right amounts of Solido and Liquex with the vitamin and mineral requirements. She goes back to the health section of the supermarket and puts more packets and cartons into her trolley. She now has 40 packets and 15 cartons. Surely this will be OK? She recalculates and finds she has 2 × 40 + 3 × 15 = 125 mg vitamins and 10 × 40 + 50 × 15 = 1150 mg minerals. Now Tanya certainly satisfies her coach’s recommendation and has even exceeded the required amounts.

Feasible solutions

The combination (40, 15) of foods will enable Tanya to satisfy the diet. This is called a possible combination, or a ‘feasible’ solution. We have seen already that (30, 5) is not a feasible solution so there is a demarcation between the two types of combinations – feasible solutions in which the diet is fulfilled and non-feasible solutions in which it is not.

Tanya has many more options. She could fill her trolley with only Solido. If she did this she would need to buy at least 88 packets. The purchase (88, 0) satisfies both requirements, because this combination would contain 2 × 88 + 3 × 0 = 176 mg vitamins and 10 × 88 + 50 × 0 = 880 mg minerals. If she bought only Liquex she would need at least 40 cartons, the feasible solution (0, 40) satisfies both vitamin and mineral requirements, because 2 × 0 + 3 × 40 = 120 mg vitamins and 10 × 0 + 50 × 40 = 2000 mg minerals. We may notice that the intake of vitamins and minerals is not met exactly with any of these possible combinations though the coach will certainly be satisfied Tanya is having enough.

Optimum solutions

Money is now brought into the situation. When Tanya gets to the checkout she must pay for the purchases. She notes that the packets and cartons are equally priced at £5 each. Of the feasible combinations we have found so far (40, 15), (88, 0) and (0, 40) the bills would be £275, £440 and £200, respectively so the best solution so far will be to buy no Solido and 40 cartons of Liquex. This will be the least cost purchase and the dietary requirement will be achieved. But how much food to buy has been hit and miss. On the spur of the moment Tanya has tried various combinations of Solido and Liquex and figured out the cost in these cases only. Can she do better? Is there a possible combination of Solido and Liquex that will satisfy her coach and at the same time cost her the least? What she would like to do is to go home and analyse the problem with a pencil and paper.

Linear programming problemsTanya’s always been coached to visualize her goals. If she can apply this to winning Olympic gold, why not to mathematics? So she draws a picture of the feasible region. This is possible because she is only considering two foods. The line AD represents the combinations of Solido and Liquex that contain exactly 120 mg vitamins. The combinations above this line have more than 120 mg vitamins. The line EC represents the combinations that contain exactly 880 mg minerals. The combinations of foods that are above both these lines is the feasible region and represents all the feasible combinations Tanya could buy.

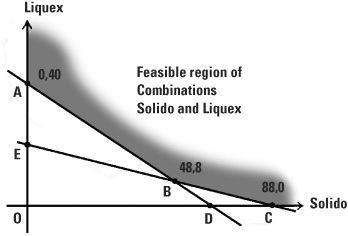
Problems with the framework of the diet problem are called linear programming problems. The word ‘programming’ means a procedure (its usage before it became synonymous with computers) while ‘linear’ refers to the use of straight lines. To solve Tanya’s problem with linear programming, mathematicians have shown that all we need to do is to work out the size of the food bill at the corner points on Tanya’s graph. Tanya has discovered a new feasible solution at the point B with coordinates (48, 8) which means that she could purchase 48 packets of Solido and 8 cartons of Liquex. If she did this she would satisfy her diet exactly because in this combination there is 120 mg of vitamins and 880 mg of minerals. At £5 for both a packet and a carton this combination would cost her £280. So the optimum purchase will remain as it was before, that is, she should purchase no Solido at all and 40 cartons of Liquex at a total cost of £200, even though she will have 1120 mg of vitamins in excess of the 880 mg required.

The optimum combination ultimately depends on the relative costs of the supplements. If the cost per packet of Solido went down to £2 and Liquex went up to £7 then the bills for the corner point combinations A (0, 40), B (48, 8) and C (88, 0) would be respectively £280, £152 and £176.

The best purchase for Tanya with these prices is 48 packets of Solido and 8 cartons of Liquex, with a bill of £152.

History

In 1947 the American mathematician George Dantzig, then working for the US Air Force, formulated a method for solving linear programming problems called the simplex method. It was so successful that Dantzig became known in the West as the father of linear programming. In Soviet Russia, cut off during the Cold War, Leonid Kantorovich independently formulated a theory of linear programming. In 1975, Kantorovich and the Dutch mathematician Tjalling Koopmans were awarded the Nobel Prize for Economics for work on the allocation of resources, which included linear programming techniques.

Tanya only considered only two foods – two variables – but nowadays problems involving thousands of variables are commonplace. When Dantzig found his method there were few computers but there was the Mathematical Tables Project – a decade-long job creation scheme which began in New York in 1938. It took a team of some ten human calculators working for 12 days with hand calculators to solve a diet problem in nine ‘vitamin’ requirements and 77 variables.

While the simplex method and its variants have been phenomenally successful, other methods have also been tried. In 1984 the Indian mathematician Narendra Karmarkar derived a new algorithm of practical significance, and the Russian Leonid Khachiyan proposed one of chiefly theoretical importance.

The basic linear programming model has been applied to many situations other than choosing a diet. One type of problem, the transportation problem, concerns itself with transporting goods from factories to warehouses. It is of a special structure and has become a field in its own right. The objective in this case is to minimize the cost of transportation. In some linear programming problems the objective is to maximize (like maximizing profit). In other problems the variables only take integer values or just two values 0 or 1, but these problems are quite different and require their own solution procedures.

It remains to be seen whether Tanya Smith wins her gold medal at the Olympic Games. If so, it will be another triumph for linear programming.

The condensed idea

Keeping healthy at least cost