Probability theory is important. It has a bearing on uncertainty and is an essential ingredient in evaluating risk. But how can a theory involving uncertainty be quantified? After all, isn’t mathematics an exact science?

The real problem is to quantify probability.

Suppose we take the simplest example on the planet, the tossing of a coin. What is the probability of getting a head? We might rush in and say the answer is ½ (sometimes expressed as 0.5 or 50%). Looking at the coin we make the assumption it is a fair coin, which means that the chance of getting a head equals the chance of getting a tail, and therefore the probability of a head is ½.

Situations involving coins, balls in boxes, and ‘mechanical’ examples are relatively straightforward. There are two main theories in the assignment of probabilities. Looking at the two-sided symmetry of the coin provides one approach. Another is the relative frequency approach, where we conduct the experiment a large number of times and count the number of heads. But how large is large? It is easy to believe that the number of heads relative to the number of tails is roughly 50:50 but it might be that this proportion would change if we continued the experiment.

But what about coming to a sensible measure of the probability of it snowing tomorrow? There will again be two outcomes: either it snows or it does not snow, but it is not at all clear that they are equally likely as it was for the coin. An evaluation of the probability of it snowing tomorrow will have to take into account the weather conditions at the time and a host of other factors. But even then it is not possible to pinpoint an exact number for this probability. Though we may not come to an actual number, we can usefully ascribe a ‘degree of belief’ that the probability will be low, medium or high. In mathematics, probability is measured on a scale from 0 to 1. The probability of an impossible event is 0 and a certainty is 1. A probability of 0.1 would mean a low probability while 0.9 would signify a high probability.

Origins of probability

The mathematical theory of probability came to the fore in the 17th century with discussions on gambling problems between Blaise Pascal, Pierre de Fermat and Antoine Gombaud (also known as the Chevalier de Méré). They found a simple game puzzling. The Chevalier de Méré’s question is this: which is more likely, rolling a ‘six’ on four throws of a dice, or rolling a ‘double six’ on 24 throws with two dice? Which option would you put your shirt on?

The prevailing wisdom of the time thought the better option was to bet on the double six because of the many more throws allowed. This view was shattered when the probabilities were analysed. Here is how the calculations go:

Throw one dice: the probability of not getting a six on a single throw is ⅚, and in four throws the probability of this would be ⅚ × ⅚ × ⅚ × ⅚ which is(⅚)⁴. Because the results of the throws do not affect each other, they are ‘independent’ and we can multiply the probabilities. The probability of at least one six is therefore

1 − (⅚)⁴ = 0.517746 . . .

Throw two dice: the probability of not getting a double six in one throw is 35/36 and in 24 throws this has the probability (35/36)²⁴.

The probability of at least one double six is therefore

1 − (35/36)²⁴ = 0.491404 . . .

We can take this example a little further.

Playing craps

The two dice example is the basis of the modern game of craps played in casinos and online betting. When two distinguishable dice (red and blue) are thrown there are 36 possible outcomes and these may be recorded as pairs (x,y) and displayed as 36 dots against a set of x/y axes – this is called the ‘sample space’.

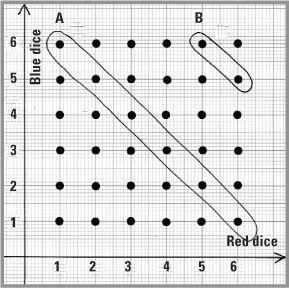
Sample space (for 2 dice)

Let’s consider the ‘event’ A of getting the sum of the dice to add up to 7. There are 6 combinations that each add up to 7, so we can describe the event by

A = {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}

and ring it on the diagram. The probability of A is 6 chances in 36, which can be written Pr(A) = 6/36 = 1/6. If we let B be the event of getting the sum on the dice equal to 11 we have the event B = {(5,6), (6,5)} and Pr(B) = 2/36 = 1/18.

In the dice game craps, in which two dice are thrown on a table, you can win or lose at the first stage, but for some scores all is not lost and you can go onto a second stage. You win at the first throw if either the event A or B occurs – this is called a ‘natural’. The probability of a natural is obtained by adding the individual probabilities, 6/36 + 2/36 = 8/36. You lose at the first stage if you throw a 2, 3 or a 12 (this is called ‘craps’). A calculation like that above gives the probability of losing at the first stage as 4/36. If a sum of either 4, 5, 6, 8, 9 or 10 is thrown, you go onto a second stage and the probability of doing this is 24/36 = 2/3.

In the gaming world of casinos the probabilities are written as odds. In craps, for every 36 games you play, on average you will win at the first throw 8 times and not win 28 times so the odds against winning on the first throw are 28 to 8, which is the same as 3.5 to 1.

The monkey on a typewriter

Alfred is a monkey who lives in the local zoo. He has a battered old typewriter with 26 keys for the letters of the alphabet, a key for a full stop, one for a comma, one for a question mark and one for a space – 30 keys in all. He sits in a corner filled with literary ambition, but his method of writing is curious – he hits the keys at random.

Any sequence of letters typed will have a nonzero chance of occurring, so there is a chance he will type out the plays of Shakespeare word perfect. More than this, there is a chance (albeit smaller) he will follow this with a translation into French, and then Spanish, and then German. For good measure we could allow for the possibility of him continuing on with the poems of William Wordsworth. The chance of all this is minute, but it is certainly not zero. This is the key point. Let’s see how long he will take to type the soliloquy in Hamlet, starting off with the opening ‘To be or’. We imagine 8 boxes which will hold the 8 letters including the spaces.

The number of possibilities for the first position is 30, for the second is 30, and so on. So the number of ways of filling out the 8 boxes is 30 × 30 × 30 × 30 × 30 × 30 × 30 × 30. The chance of Alfred getting as far as ‘To be or’ is 1 chance in 6.561 × 10¹¹. If Alfred hits the typewriter once every second there is an expectation he will have typed ‘To be or’ in about 20,000 years, and proved himself a particularly long-lived primate. So don’t hold your breath waiting for the whole of Shakespeare. Alfred will produce nonsense like ‘xo,h?yt?’ for a great deal of the time.

How has the theory developed?

When probability theory is applied the results can be controversial, but at least the mathematical underpinnings are reasonably secure. In 1933, Andrey Nikolaevich Kolmogorov was instrumental in defining probability on an axiomatic basis – much like the way the principles of geometry were defined two millennia before.

Probability is defined by the following axioms:

1. the probability of all occurrences is 1

2. probability has a value which is greater than or equal to zero

3. when occurrences cannot coincide their probabilities can be added

From these axioms, dressed in technical language, the mathematical properties of probability can be deduced. The concept of probability can be widely applied. Much of modern life cannot do without it. Risk analysis, sport, sociology, psychology, engineering design, finance, and so on – the list is endless. Who’d have thought the gambling problems that kick-started these ideas in the 17th century would spawn such an enormous discipline? What were the chances of that?

the condensed idea

The gambler’s secret system