Distribution Function

The distribution function 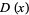, also called the cumulative distribution function (CDF) or cumulative frequency function, describes the probability that a variate  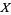takes on a value less than or equal to a number . The distribution function is sometimes also denoted 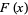 (Evans et al. 2000, p. 6).

The distribution function is therefore related to a continuous probability density function 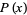 by

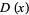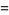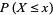			(1)
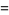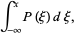			(2)

so 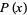 (when it exists) is simply the derivative of the distribution function

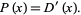(3)

Similarly, the distribution function is related to a discrete probabilit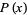y  by

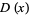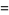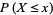			(4)
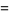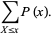			(5)

There exist distributions that are neither continuous nor discrete.

A joint distribution function can be defined if outcomes are dependent on two parameters:

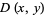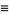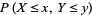			(6)
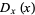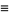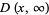			(7)
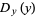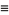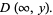			(8)

Similarly, a multivariate distribution function can be defined if outcomes depend on 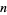 parameters:

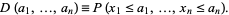(9)

The probability content of a closed region can be found much more efficiently than by direct integration of the probability density function 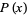 by appropriate evaluation of the distribution function at all possible extrema defined on the region (Rose and Smith 1996; 2002, p. 193). For example, for a bivariate distribution function 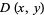, the probability content in the region 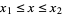,  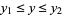is given by

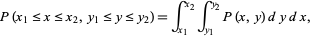(10)

but can be computed much more efficiently using

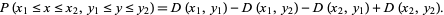(11)

Given a continuous 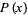, assume you wish to generate numbers distributed as  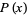using a random number generator. If the random number generator yields a uniformly distributed value  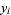in  for each trial 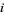, then compute

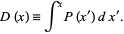(12)

The formula connecting 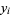 with a variable distributed as  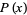is then

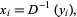(13)

where 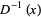 is the inverse function of 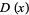. For example, if  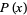were a normal distribution so that

(14)

then

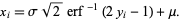(15)

A distribution with constant variance of 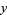 for all values of  is known as a homoscedastic distribution. The method of finding the value at which the distribution is a maximum is known as the maximum likelihood method.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Probability Functions." Ch. 26 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 925-964, 1972.

Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, pp. 6-8, 2000.

Iyanaga, S. and Kawada, Y. (Eds.). "Distribution of Typical Random Variables." Appendix A, Table 22 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1483-1486, 1980.

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 92-94, 1984.

Rose, C. and Smith, M. D. "The Multivariate Normal Distribution." Mathematica J. 6, 32-37, 1996.

Rose, C. and Smith, M. D. Mathematical Statistics with Mathematica. New York: Springer-Verlag, 2002.