


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-4-2021
Date: 2-5-2021
Date: 22-2-2021
|
Given a subset 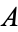 of a larger set, the characteristic function
of a larger set, the characteristic function 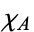 , sometimes also called the indicator function, is the function defined to be identically one on
, sometimes also called the indicator function, is the function defined to be identically one on 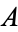 , and is zero elsewhere. Characteristic functions are sometimes denoted using the so-called Iverson bracket, and can be useful descriptive devices since it is easier to say, for example, "the characteristic function of the primes" rather than repeating a given definition. A characteristic function is a special case of a simple function.
, and is zero elsewhere. Characteristic functions are sometimes denoted using the so-called Iverson bracket, and can be useful descriptive devices since it is easier to say, for example, "the characteristic function of the primes" rather than repeating a given definition. A characteristic function is a special case of a simple function.
The term characteristic function is used in a different way in probability, where it is denoted 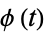 and is defined as the Fourier transform of the probability density function using Fourier transform parameters
and is defined as the Fourier transform of the probability density function using Fourier transform parameters 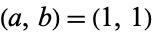 ,
,
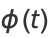 |
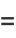 |
](https://mathworld.wolfram.com/images/equations/CharacteristicFunction/Inline8.gif) |
(1) |
 |
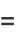 |
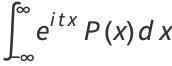 |
(2) |
 |
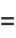 |
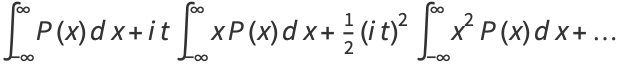 |
(3) |
 |
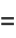 |
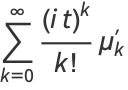 |
(4) |
 |
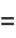 |
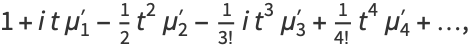 |
(5) |
where 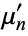 (sometimes also denoted
(sometimes also denoted 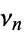 ) is the
) is the 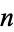 th moment about 0 and
th moment about 0 and 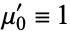 (Abramowitz and Stegun 1972, p. 928; Morrison 1995).
(Abramowitz and Stegun 1972, p. 928; Morrison 1995).
A statistical distribution is not uniquely specified by its moments, but is by its characteristic function if all of its moments are finite and the series for its characteristic function converges absolutely near the origin (Papoulis 1991, p. 116). In this case, the probability density function is given by
=1/(2pi)int_(-infty)^inftye^(-itx)phi(t)dt](https://mathworld.wolfram.com/images/equations/CharacteristicFunction/NumberedEquation1.gif) |
(6) |
(Papoulis 1991, p. 116).
The characteristic function can therefore be used to generate raw moments,
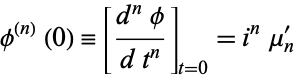 |
(7) |
or the cumulants 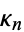 ,
,
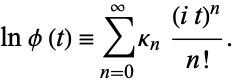 |
(8) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 928, 1972.
Kenney, J. F. and Keeping, E. S. "Moment-Generating and Characteristic Functions," "Some Examples of Moment-Generating Functions," and "Uniqueness Theorem for Characteristic Functions." §4.6-4.8 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 72-77, 1951.
Morrison, K. E. "Cosine Products, Fourier Transforms, and Random Sums." Amer. Math. Monthly 102, 716-724, 1995.
Papoulis, A. "Characteristic Functions." §5-5 in Probability, Random Variables, and Stochastic Processes, 3rd ed. New York: McGraw-Hill, 1991.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|