المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Correlation Ratio |
 1536
 03:28 مساءً
date: 28-3-2021 |
Author : Kenney, J. F. and Keeping, E. S. 
Book or Source : Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951. 
Page and Part : ...|
Read More
Date: 1-5-2021
3190
Date: 15-4-2021
2248
Date: 14-2-2021
2455
|
Let there be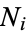 
observations of the 
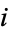th phenomenon, where 
, ..., 
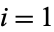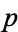and
 |
 |
 |
(1) |
 |
 |
 |
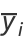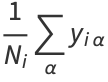(2) |
 |
 |
 |
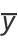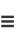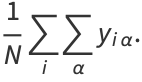(3) |
Then the sample correlation ratio is defined by
 |
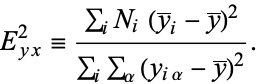(4) |
Let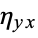 
be the population correlation ratio. If 
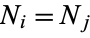for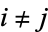 
, then
 |
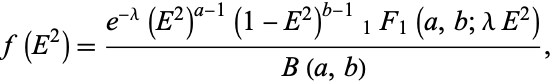(5) |
where
 |
 |
 |
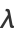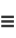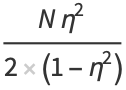(6) |
 |
 |
 |
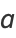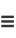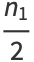(7) |
 |
 |
 |
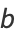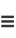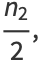(8) |
and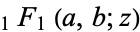 
is the confluent hypergeometric limit function. If 
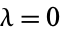, then
 |
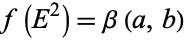(9) |
(Kenney and Keeping 1951, pp. 323-324).
REFERENCES:
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|
