المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Rational Approximation |
 753
 01:09 صباحاً
date: 17-10-2020 |
Author : Hilbert, D. and Cohn-Vossen, S 
Book or Source : Geometry and the Imagination. New York: Chelsea 
Page and Part : p. 41|
Read More
Date: 1-11-2020
557
Date: 14-11-2019
651
Date: 10-11-2020
744
|
If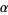 
is any number 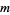and 
and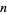 
are integers, then there is a rational number 
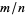for which
 |
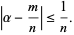(1) |
If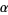 
is irrational and 
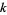is any whole number, there is a fraction 
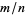with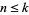 
and for which
 |
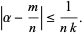(2) |
Furthermore, there are an infinite number of fractions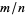 
for which
 |
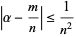(3) |
(Hilbert and Cohn-Vossen 1999, pp. 40-44).
Hurwitz has shown that for an irrational number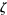 
 |
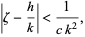(4) |
there are infinitely rational numbers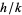 
if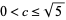 
, but if 
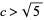, there are some 
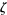for which this approximation holds for only finitely many 
.
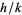REFERENCES:
Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 41, 1999.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
