Spin-Spin Coupling

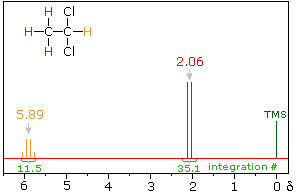
The spin-spin interaction of neighboring hydrogens takes place through the covalent bonds that join them. The most common bonding relationship is vicinal (joined by three sigma bonds). In this case a neighboring proton having a +1/2 spin shifts the resonance frequency of the proton being observed to a slightly higher value (up to 7 Hz), and a ^_1/2 neighboring spin shifts it to a lower frequency. Remember that the total population of these two spin states is roughly equal, differing by only a few parts per million in a strong magnetic field. If several neighboring spins are present, their effect is additive.
In the spectrum of 1,1-dichloroethane shown on the right, it is clear that the three methyl hydrogens (red) are coupled with the single methyne hydrogen (orange) in a manner that causes the former to appear as a doublet and the latter as a quartet. The light gray arrow points to the unperturbed chemical shift location for each proton set.
The statistical distribution of spins within each set explains both the n+1 rule and the relative intensities of the lines within a splitting pattern. The action of a single neighboring proton is easily deduced from the fact that it must have one of two possible spins. Interaction of these two spin states with the nuclei under observation leads to a doublet located at the expected chemical shift. The corresponding action of the three protons of the methyl group requires a more detailed analysis. In the display of this interaction four possible arrays of their spins are shown. The mixed spin states are three times as possible as the all +1/2 or all ^_1/2 collection. Consequently, we expect four signals, two above the chemical shift and two below it. This spin analysis also suggests that the intensity ratio of these signals will be 1:3:3:1. The line separations in splitting patterns are measured in Hz, and are characteristic of the efficiency of the spin interaction; they are referred to as coupling constants (symbol J). In the above example, the common coupling constant is 6.0 Hz.

Multiplicity	Relative Line Intensity
singlet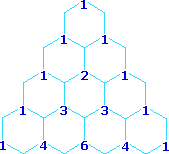
doublet
triplet
quartet
quintet

A simple way of estimating the relative intensities of the lines in a first-order coupling pattern is shown on the right. This array of numbers is known as Pascal's triangle, and is easily extended to predict higher multiplicities. The number appearing at any given site is the sum of the numbers linked to it from above by the light blue lines. Thus, the central number of the five quintet values is 3 + 3 = 6. Of course, a complete analysis of the spin distributions, as shown for the case of 1,1-dichloroethane above, leads to the same relative intensities.

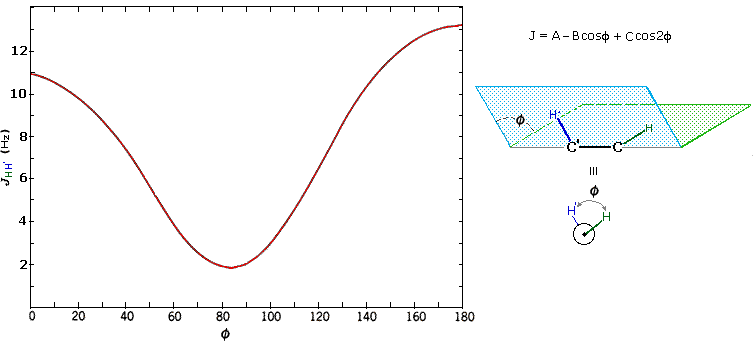
Coupling constants are independent of the external magnetic field, and reflect the unique spin interaction characteristics of coupled sets of nuclei in a specific structure. As noted earlier, coupling constants may vary from a fraction of a Hz to nearly 20 Hz, important factors being the nature and spatial orientation of the bonds joining the coupled nuclei. In simple, freely rotating alkane units such as CH₃CH₂X or YCH₂CH₂X the coupling constant reflects an average of all significant conformers, and usually lies in a range of 6 to 8 Hz. This conformational mobility may be restricted by incorporating the carbon atoms in a rigid ring, and in this way the influence of the dihedral orientation of the coupled hydrogens may be studied.

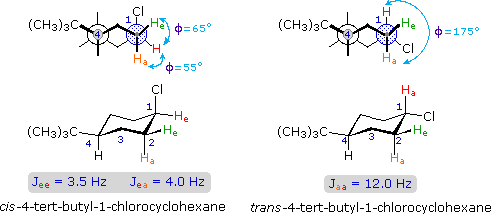
The structures of cis and trans-4-tert-butyl-1-chlorocyclohexane, shown above, illustrate how the coupling constant changes with the dihedral angle (φ) between coupled hydrogens. The inductive effect of chlorine shifts the resonance frequency of the red colored hydrogen to a lower field (δ ca. 4.0), allowing it to be studied apart from the other hydrogens in the molecule. The preferred equatorial orientation of the large tert-butyl group holds the six-membered ring in the chair conformation depicted in the drawing. In the trans isomer this fixes the red hydrogen in an axial orientation; whereas for the cis isomer it is equatorial. The listed values for the dihedral angles and the corresponding coupling constants suggest a relationship, which has been confirmed and clarified by numerous experiments. This relationship is expressed by the Karplus equation shown below.

Geminal couplings are most commonly observed in cyclic structures, but are also evident when methylene groups have diastereomeric hydrogens.