To a first and good approximation the lensing properties of the mass distribution in the Galactic Center can be described as those of a point mass, the MBH. Figure 1.1 shows the light ray diagram of lensing by a point mass in the small-angle limit. The bending angle is given by

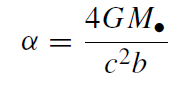 (1.1)

where b is the impact parameter of the light ray with respect to the lens. Note that unlike a spherical glass lens, where the bending angle is zero when the ray goes through the lens center and increases with the impact parameter, the bending angle of a gravitational lens diverges toward the center and decreases with the impact parameter. It is therefore not surprising that a gravitational lens does not produce a faithful image of the lensed source, but rather breaks, warps and/or flips the image. A point lens creates two images of the source, one on either side of the lens. There are always two images in focus at the observer, regardless of the distance of the source behind the lens. The two images, the lens and the (unobserved) source all lie on one line. The typical angular cross section of the lens is given by the Einstein angle,

 (1.2)

where D_OL is the observer-lens distance, D_LS is the lens-source distance, and D_OS is the observer-source distance.

The relation between the angular position of the source relative to the observer-lens axis (the optical axis) can be derived from the geometry of the light paths,

 y = x_1,2 − 1/x_1,2    (1.3)

where x_1,2 and y are measured in terms of θ_E and where x₂ < 0 by definition. Gravitational lensing conserves surface brightness, and so the magnifications A_1,2 in the flux of each image relative to that of the unlensed source are proportional to change in the angular area of the source,

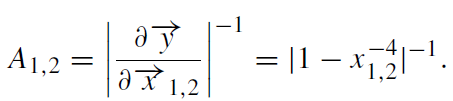 (1.4)

The primary image at x₁ is always magnified. The secondary image at x₂ can be demagnified to zero. The two magnifications obey the relations

 A₁ = A₂ + 1 ≥ 1      (1.5)

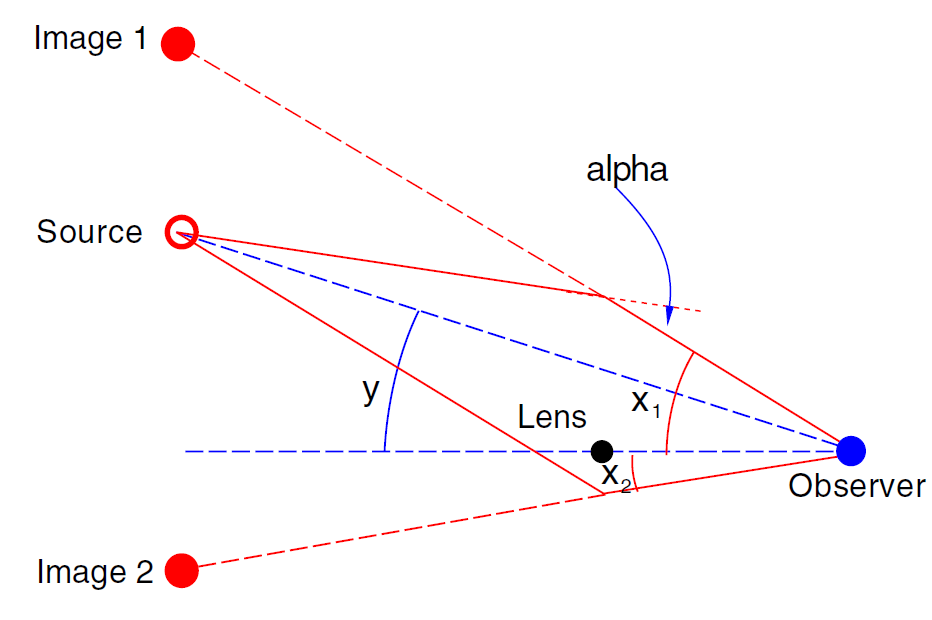
Figure 1.1. The light ray diagram for lensing by a point mass. The light rays from a source, at angular position y relative to the observer-lens optical axis, are bent by the gravitational lens and reach the observer from angles x₁ and x₂, thereby appearing as two images. Unlike a spherical glass lens, the light bending angle α of a gravitational lens is inversely proportional to the impact parameter to the lens.

and

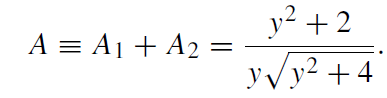 (1.6)

When y = 0 the magnification formally diverges and the image appears as a ring of angular size θ_E, the Einstein ring. This divergence is avoided in practice by the finite size of the source (e.g. a star). Finite-sized sources are also sheared tangentially around the Einstein ring as the magnification increases. In the limit of high magnification or small source angle,

A ∼ 1/y      (y <<1). (1.7)