In   last sections we developed many properties of functions from R¹ into R¹ with the purpose of proving the basic theorems in differential and integral calculus of one variable. The next step in analysis is the establishment of the basic facts needed in proving the theorems of calculus in two and more variables. One way would be to prove extensions of the theorems of Chapters2–5 for functions from R² into R¹, then for functions from R³ into R¹, and so forth. However, all these results can be encompassed in one general theory obtained by introducing the concept of a metric space and by considering functions with domain in one metric space and with range in a second metric space. In this chapter we introduce the fundamentals of this theory, and in the following chapters we apply the results to differentiation and integration in Euclidean space in any number of dimensions.

We establish a simple version of the Schwarz inequality, one of the most useful inequalities in analysis.

Theorem 1.1 (Schwarz inequality)

Let x = (x₁,x₂,...,x_N) and y = (y₁,y₂,...,y_N) be elements of R^N. Then(1.1)

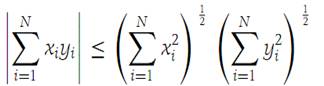
The equality sign holds if and only if either all the xi are zero or there is a number λ such that y_i =λx_i for i =1,2,...,N.

Proof

If every x_i is zero, then the equality sign in expression (1.1) holds. Assume that there is at least one x_i not zero. We form the function

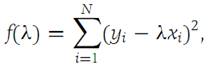
which is nonnegative for all values of λ. We set

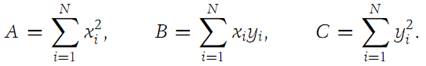
Then clearly,

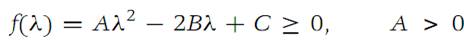
From elementary calculus it follows that the nonnegative minimum value of the quadratic function f(λ) is

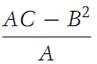
The statement AC−B² ≥ 0 is equivalent to expression (1.1). The equality sign in expression (1.1) holds if f(λ) = 0 for some value of λ, say λ₁;in this case y_i − λ₁x_i =0 for every i.

We recall that in the Euclidean plane the length of any side of a triangle is less than the sum of the lengths of the other two sides. A generalization of this fact is known as the Triangle inequality. It is proved by means of a simple application of the Schwarz inequality.

Theorem 1.2 (Triangle inequality)

Let x = (x₁,x₂,...,x_N) and y = (y₁,y₂,...,y_N) be elements of R^N. Then(1.2)

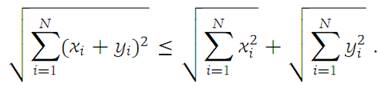
The equality sign in expression (1.2) holds if and only if either all the x_i are zero or there is a nonnegative number λ such that y_i =λx_i for i =1,2,...,N.

Proof

We have

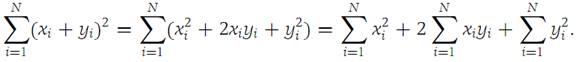
We apply the Schwarz inequality to the middle term on the right, obtaining

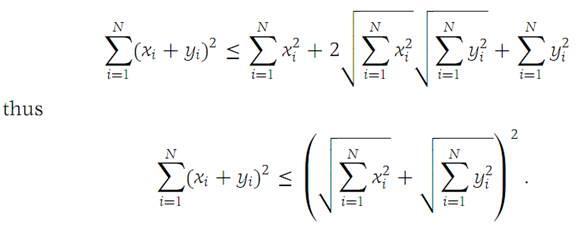
Since the left side of this inequality is nonnegative, we may take the square root to obtain expression (1.2). If all xi are zero, then equality in expression (1.2) holds. Otherwise, equality holds if and only if it holds in the application of Theorem 1.1. The nonnegativity of λ isrequired to ensure that 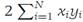 has all nonnegative terms when we set y_i = λx_i .

Corollary

Let x = (x₁,x₂,...,x_N), y = (y₁,y₂,...,y_N), and z = (z₁,z₂,...,z_N) be elements of R^N. Then(1.3)

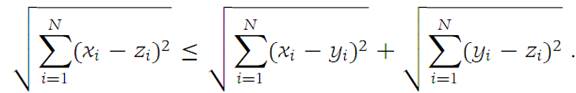
The equality sign in expression (1.3) holds if and only if there is a number r with 0 ≤ r ≤ 1 such that y_i = rx_i + (1 − r)z_i for i = 1,2,...,N.

Proof

Setting a_i = x_i −y_i and b_i = y_i −z_i for i =1, 2,...,N, we see that inequality (1.3) reduces to inequality (1.2) for the elements a =(a₁,...,a_N) and b = (b₁,b₂,...,b=). The number r is λ₁/(1 + λ₁) in Theorem 1.1.

Remark

The corollary to Theorem 1.2 is the familiar assertion that the sum of the lengths of any two sides of a triangle exceeds the length of the third side in Euclidean N-dimensional space. In this chapter we shall be concerned with sets or collections of elements, which may be chosen in any manner whatsoever. A set will be considered fully described whenever we can determine whether or not any given element is a member of the set.

Definition

Let S and T be sets. The Cartesian product of S and T, denoted by S × T, is the set of all ordered pairs (p, q) in which p ∈ S and q ∈ T. The Cartesian product of any finite number of sets S₁,S₂,...,S_N is the set o ordered N-tuples (p₁,p₂,...,p_N) in which p_i ∈ S_i for i = 1, 2,...,N. We write S₁ × S₂ ×···× S_N.

Examples

(1) The space R^N is the Cartesian product R¹ × R¹ ×···× R¹ (N factors).

(2) The Cartesian product of I₁ ={x : a ≤ x ≤ b} and I₂ ={x : c ≤ x ≤ d} Is the rectangle T ={(x, y) : a ≤ x ≤ b, c ≤ x ≤ d}. That is,

T =I₁ × I₂.

Definition

Let S be a set and suppose d is a function with domain consisting of all pairs of points of S and with range in R¹. That is, d is a function from S×S into R¹. We say that S and the function d form a metric space when the function d satisfies the following conditions

(i) d(x, y) ≥ 0 for all (x, y) ∈ S ×S; and d(x, y) = 0 if and only if x= y.

(ii) d(y, x) = d(x, y)   for all (x, y) ∈ S × S.

(iii) d(x, z) ≤ d(x, y) + d(y, z) for all (x, y, z) ∈ S. (Triangle inequality.) The function d satisfying conditions (i), (ii), and (iii) is called the metric, or distance, function in S. Hence a metric space consists of the pair(S, d).

Examples of metric spaces

1. In the space R^N, choose

where x= (x₁,x₂,...,x_N) and y = (y₁,y₂,...,y_N). The function d is a metric. Conditions(i) and (ii) are obvious, while (iii) is precisely the content of the corollary to Theorem 1.2. The pair (R^N,d ) isa metric space. This metric, known as the Euclidean metric, is the familiar one

employed in two- and three-dimensional Euclidean geometry.

1. In the space R^N, choose

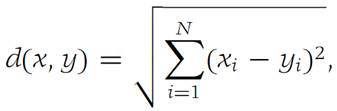
where x =(x₁,x₂,...,x_N) and y = (y₁,y₂,...,y_N). The reader can verify that d₁ is a metric. Therefore, (R^N,d₁) is a metric space. We observe that this metric space is different from the space (R^N,d) exhibited in the first example.

1. Let C be the collection of all continuous functions that have I ={x :0 ≤ x ≤ 1} for domain and have range in R¹. For any two elements f, g in C, define

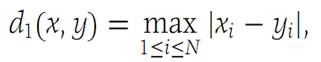
It is not difficult to verify that d isa metric. Hence (C, d) is a metric space.

Examples 1 and 2 above show that a given set may become a metric space in a variety of ways. Let S be a given set and suppose that (S, d₁) and (S, d₂) are metric spaces. We define the metrics d₁ and d₂ as equivalent if there are positive constants c and C such that

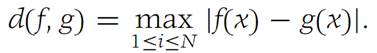
for all x, y in S. It is not difficult to show that the metrics in Examples1 and 2 are equivalent.

1. Show that (R^N,d₁) is a metric space where

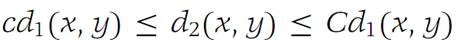
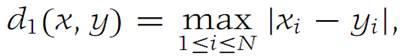
2. Suppose that (S, d) is a metric space. Show that (S, d^/) is a metric space, where

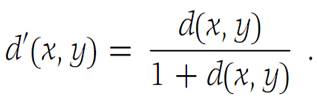
[Hint: Show first that d(x, z) = λ[d(x, y) + d(y, z)] for some λ with 0 ≤ λ ≤ 1.]

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(101-106)