In the definition of continuity of a function f at a point x₀, it is necessary to obtain a number δ for each positive number ε prescribed in advance  The number δ, which naturally depends on ε, also depends on the particular value x₀. Under certain circumstances it may happen that the same value δ may be chosen for all points x in the domain. Then we say that f is uniformly continuous.

Definition

A function f with domain S is said to be uniformly continuous on S if for every ε> 0 there is a δ> 0 such that

                        |f(x₁) − f(x₂)| <ε    whenever  |x₁ − x₂| <δ

and   x₁,x₂  are in S. The important condition of uniform continuity states that the same value of δ holds for all x₁,x₂ in S.

Among the properties of continuous functions used in proving the basic theorems of integral calculus, that of uniform continuity plays a central role. The principal result of this section (Theorem 1.1 below) shows that under rather simple hypotheses continuous functions are uniformly continuous.

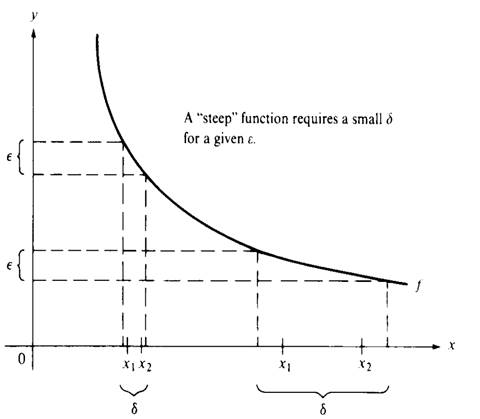
                                                   Figure 1.1

A function may be continuous on a set S without being uniformly continuous. As Figure 1.1 shows, once an ε is given, the value of δ required n the definition of ordinary continuity varies according to the location of x₁ and x₂; the “steeper” the function, the smaller the value of δ required. As an example of a continuous function that is not uniformly continuous, consider

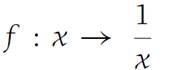
defined on the set S ={x :0 <x ≤ 1}. It is clear that f is continuous for each x in S. However, with ε any positive number, say 1, we shall show

there is no number δ such that

                             |f(x₁) − f(x₂)| < 1 whenever |x₁ − x₂| <δ

for all x₁,x₂ in S. To see this we choose x₁ = 1/n and x₂ = 1/(n + 1) for a positive integer n. Then |f(x₁) − f(x₂)|=|n − (n + 1)|= 1; also, we have |x₁ − x₂|= 1/(n(n + 1)).If n is very large, then x₁ and x₂ are close together. Therefore, if a δ is given, simply choose n so large that x₁ and x₂ are closer together than δ. The condition of uniform continuity is violated, since f(x₁) and f(x₂) may not be “close.”

An example of a uniformly continuous function on a set S is given by(1.6)

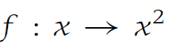
on the domain S ={x :0 ≤ x ≤ 1}. To see this, suppose ε> 0 is given.

We must find a δ> 0 such that

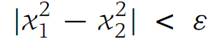
whenever |x₁ − x₂| <δ

for all x₁,x₂ in S. To accomplish this, choose δ = ε/2. Then, because 0 ≤ x1 ≤ 1 and 0 ≤ x2 ≤ 1, we have

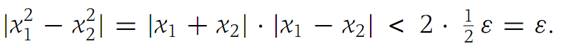
This inequality holds for all x₁,x₂ on [0, 1] such that |x₁ − x₂| <δ.

The same function (1.6) above defined on the domain S₁ ={x :0 ≤ x< ∞} is not uniformly continuous there. To see this, suppose ε> 0 Is given. Then for any δ> 0, choose x₁,x₂ such that x₁ − x₂ = δ/2 and x₁ + x₂ = 4ε/δ. Then we have

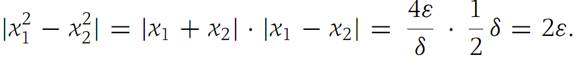
The condition of uniform continuity is violated for this x₁,x₂. An important criterion for determining when a function is uniformly continuous is established in the next result.

Theorem 1.1 (Uniform continuity Theorem)

If f is continuous on the closed interval I ={x:a ≤ x ≤ b}, then f is uniformly continuous on I.

Proof

We shall suppose that f is not uniformly continuous on I and reach a contradiction. If f is not uniformly continuous, there is an ε0 > 0for which there is no δ> 0 with the property that |f(x₁) − f(x₂)| <ε0 for all pairs x₁,x₂ ∈ I and such that |x₁ − x₂| <δ. Then for each positive integer n, there is a pair x^/_n,x^//_n on I such that(1.7)

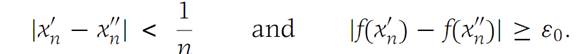
From the Bolzano–Weierstrass theorem, it follows that there is a subse-quence of {x^/_n}, which we denote {x^/_kn}, convergent to some number x₀ in I. Then, since |x^/_kn− x^//_kn| < 1/n, we see that x^//_kn→ x₀ as n →∞. Using the fact that f is continuous on I, we havef(x^/_kn) → f(x₀), f(x^//_kn) → f(x₀).

That is, there are positive integers N1 and N2 such that

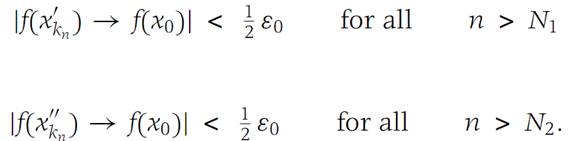
Hence for all n larger than both N₁ and N₂ we find

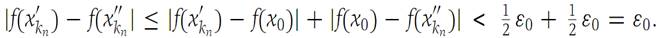
This last inequality contradicts (1.7), and the result is established. As the example of the function f : x → 1/x shows, the requirement that I be a closed interval is essential. Also, the illustration of the function f : x → x₂ on the set S₁ ={x :0 ≤ x< ∞} shows that Theorem1.11 does not apply if the interval is unbounded. It may happen that continuous functions are uniformly continuous on unbounded sets. But these must be decided on a case-by-case basis. See Problems 3 and 4 at the end of the section.

Problems

1. Suppose that f is a continuous, increasing function on a closed interval    I ={x : a ≤ x ≤ b}. Show that the range of f is the interval [f(a), f(b)].

2. Suppose that f is uniformly continuous on the closed intervals I₁

and I₂. Show that f is uniformly continuous on S = I₁ ∪ I₂.

3. Show that the function f : x → 1/x is uniformly continuous on S ={x :1 ≤ x< ∞}.

Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(57-60)