There are two principal extensions to RN of the theory of differentiation of real-valued functions on R¹. In this section, we develop the natural generalization of ordinary differentiation discussed in (Elementary Theory of Differentiation)to partial differentiation of functions from RN to R1. In Section of (The Derivative in R^N .), we extend the ordinary derivative to the total derivative. We shall use letters x, y, z, etc. to denote elements in RN. The components of an element x are designated by (x₁,x₂,...,x_N), and as usual, the Euclidean distance, given by the formula

will be used. We also write d(x, y) =|x − y| and d(x, 0) =|x|.

Definition

Let f be a function with domain an open set in R^N and range in R¹.We define the N functions f ,i with i = 1, 2,...,N by the formulas

whenever the limit exists. The functions f_,1,f_,2,...,f_,N are called the first partial derivatives of  f .

We assume that the reader is familiar with the elementary processes of differentiation. The partial derivative with respect to the ith variable Is computed by holding all other variables constant and calculating the ordinary derivative with respect to x_i . That is, to compute f_,i at the value a = (a₁,a₂,...,a_N), form the function ϕ (from R¹ to R¹) by setting

(1.1)

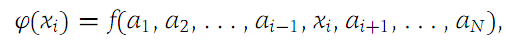
and observe that (1.2)

There are many notations for partial differentiation. In addition to the one above, the most common ones are

Good notation is important in studying partial derivatives, since them any letters and subscripts that occur can lead to confusion. The two “best” symbols, especially in discussing partial derivatives of higher order, are f_,i and Di f , and we shall employ these most of the time. We recall that the equations of a line segment in RN connecting the points a = (a₁,...,a_N) and a + h = (a₁ + h₁,...,a_N + h_N) are given parametrically by the formulas(the parameter is t)

The next theorem isthe extension to functions from R^N to R¹ of the Mean-value theorem.

Theorem 1.1 (Extended Mean-value theorem)

Let τ_i be the line segment in R^N connecting the points (a₁,a₂,...,a_i ,...,a_N) and (a₁,a₂,...,a_i +h_i ,...,a_N). Suppose f is a function from R^N into R¹ with domain containing τ_i , and suppose that the domain of f_,i contains τ_i . Then there is a real number ξ_i on the closed interval in R¹ with endpoints a_i and a_i + h_i such that (1.3)

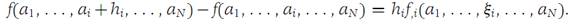
Proof

If h_i = 0, then equation (1.3) holds. If h_i = 0, we use the notation of expression (1.1) to write the left side of equation (1.3) in the form

For this function on R , we apply the Mean-value theorem   to conclude that

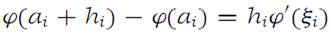
This formula is a restatement of equation (1.3). (Theorem of(Fundamental lemma of differentiation) Suppose that f has a derivative at x₀. Then there is a function η defined in aninterval about 0 such that    f(x₀ + h) − f(x₀) = [f^/(x₀) + η(h)] · h. Also, η is continuous at 0 with η(0) = 0.)),

 the Fundamental lemma of differentiation, has the following generalization for functions from R^N into R¹.We state the theorem in the general case and prove it for N= 2.

Theorem 1.2 (Fundamental lemma of differentiation)

Suppose that the functions f and f_,1,f_,2,...,f_,N all have a domain in R^N that contains an open ball about the point a = (a₁,a₂,...,a_N). Suppose all the f_,I i = 1,2,...,N, are continuous at a. Then

(a) f is continuous at a;

(b) there are functions Ԑ₁(x), Ԑ₂(x),...,Ԑ_N(x), continuous at x= 0, such

that Ԑ₁(0) =Ԑ₂(0) = ... = Ԑ_N(0) = 0 and(1.4)

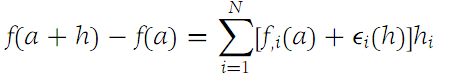
for h = (h₁,h₂,...,h_N) in some ball B(0,r) in RN of radius r and center at h = 0.

Proof

For N =2. We employ the identity (1.5)

Since f, f_,1, and f_,2 are defined in an open ball about a =(a₁,a₂), this identity is valid for h₁,h₂ in a sufficiently small ball (of radius, say, r) about h₁ = h₂ = 0. Applying Theorem 1.1 to the right side of equation (1.5), we find that there are numbers ξ₁(h₁,h₂), ξ₂(h₁,h₂) on the closed intervals from a₁ to a₁ + h₁ and from a₂ to a₂ + h₂, respectively, such that (1.6)

Equation (1.6) is valid for h₁,h₂ in the ball of radius r about h₁ = h₂ = 0.

Now define(1.7)

We wish to show that Ԑ₁ and Ԑ₂ are continuous at (0, 0). Let Ԑ> 0 be given

Since f_,1 and f= are continuous at (a₁,a₂), there is a δ> 0 such that)1.8)

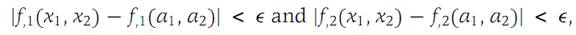
for (x₁,x₂) in a ball of radius δ with center at (a₁,a₂). Comparing expressions (1.7) and (1.8), we see that if h₁ and h₂ are sufficiently small (so that (ξ₁,ξ₂) is close to (a₁,a₂)), then

Moreover, Ԑ₁₍0, 0) =0 and Ԑ₂(0, 0) =0. Substituting the values of Ԑ₁ and Ԑ₂ from equations (1.7) into equation (1.6) we obtain part (b) of the theorem. The continuity of f at (a₁,a₂) follows directly from Equation (1.4).

The proof for N> 2 is similar.

The chain rule for ordinary differentiation can be extended to provide a rule for taking partial derivatives of composite functions. We establish the result for a function f : R^N → R¹ when it is composed with N functions g₁,g₂,...,g_N each of which is a mapping from R^M into R¹. The integer M may be different from N. If Y= (y₁,y₂,...,y_N) and x =(x₁,x₂,...,x_M) are elements of R^N and R^M, respectively, then in customary terms, we wish to calculate the derivative of H(x)  (a function from R^M into R¹) with respect to x_j , where                          f= f(y₁,y₂,...,y_N) and

(1.9)           H(x) =f [g¹(x), g²(x),...,g^N(x)].

Theorem 1.3 (Chain rule)

Suppose that each of the functions g₁,g₂,...,g_N is amapping  from R^M into R¹.

For a fixed integer j between 1 and M, assume that g¹_,j,g²_,j,...,g^N_,j are defined at some point b = (b₁,b₂,...,b_M). Suppose that f and its partial derivatives f_,1,f_,2,...,f_,N are continuous at the point a = (g¹(b),g²(b),...,g^N(b)). Form the function H as in equation (1.9). Then the partial derivative of H with respect to x_j isgiven by

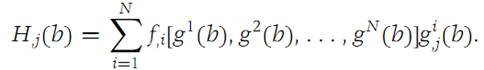
Proof

Define the following functions from R₁ into R₁.

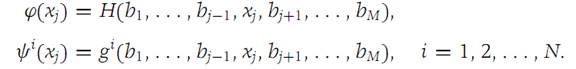
Then, according to equation (1.9), we have

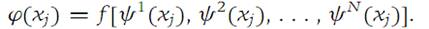
With h denoting a real number, define

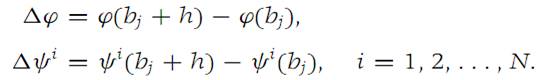
Since each ψⁱ is continuous at b_j , it follows that Δψⁱ → 0as h → 0. We apply equation (1.4) from Theorem 1.2 to the function ϕ and use Δψⁱ instead of hi in that equation. We obtain(1.10)

In this formula, we have Ԑ_i= Ԑ_i(Δψ¹,...,Δψ^N) and Ԑⁱ → 0as Δψ^k → 0, K= 1, 2,...,N.

Now write equation (1.10) in the form

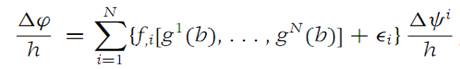
valid for |h| sufficiently small. Letting h tend to 0, we get the statement of the Chain rule.

Problems

1. Let D be a ball in R^N and suppose f : D → R¹ has the property that f_,1 = f_,2 =···= f_,N = 0 for all x ∈ D. Show that f ≡ constant in D.

2. Let f : R^N → R¹ be given and suppose that g¹,g²,...,g^N are N functions from R^M into R¹. Let h¹,h²,...,h^M be M functions from R^p into R¹. Give a formula for the Chain rule for H^,i(x), where

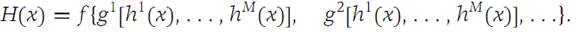
3. Write a proof of Theorem 1.2for N =3.

         Basic Elements of Real Analysis, Murray H. Protter, Springer, 1998 .Page(125-129)