


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 14-8-2016
Date: 18-8-2016
Date: 6-9-2016
|
Two-Delta-Function Scattering
A free particle of mass m, traveling with momentum parallel to the z-axis, scatters off the potential
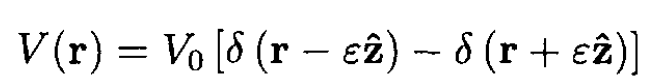
Calculate the differential scattering cross section, dσ/dΩ, in the Born approximation. Does this approximation provide a reasonable description for scattering from this potential? In other words, is it valid to use unperturbed wave functions in the scattering amplitude?
SOLUTION
Let us take an unperturbed wave function of the particle of the form
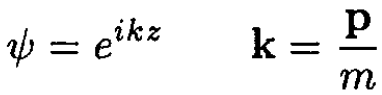 (1)
(1)
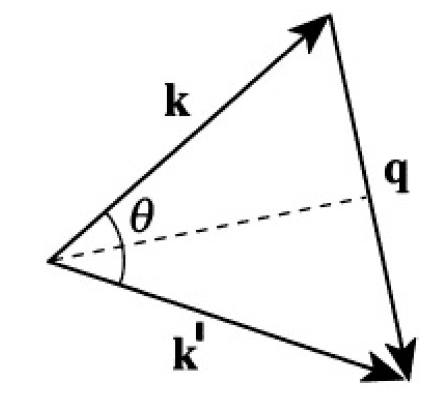
Figure 1.1
Suppose that, after scattering, the wave vector becomes k'. In the Born approximation, the scattering amplitude f (θ) is
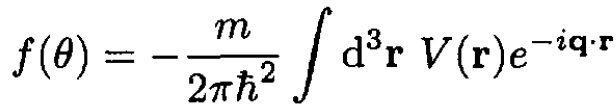 (2)
(2)
where q = k' - k and q = 2k sin(θ/2) (see Figure 1.1). Substituting the potential V(r) into (2), we obtain
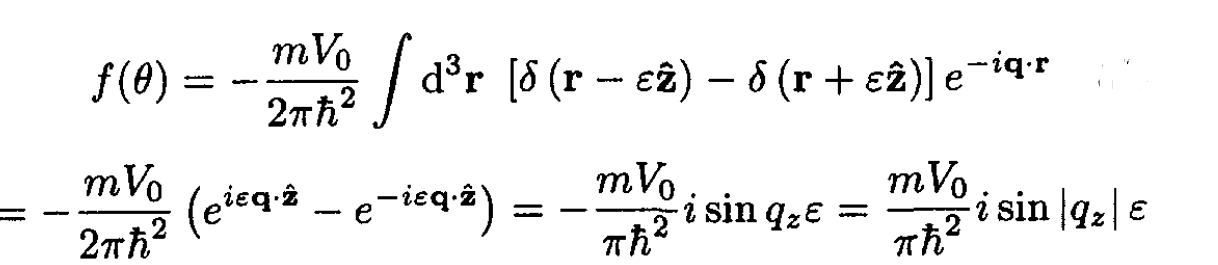 (3)
(3)
where qz = -q sin(θ/2) = -2ksin2(θ/2) is the projection of the vector q on the z axis. The scattering cross section
 (4)
(4)
In order to apply the Born approximation, i.e., to use perturbation theory, we must satisfy at least one of two conditions:
 (5)
(5)
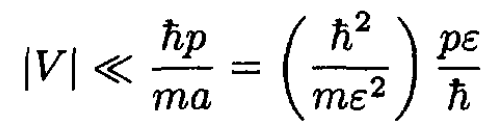 (6)
(6)
where a = ε is the range of the potential. The first condition derives from the requirement that the perturbed wave function be very close to the unperturbed wave function. Inequality (5) may also be considered the requirement that the potential be small compared to the kinetic energy of the particle localized at the source of the perturbation. Even if the first condition is not satisfied, particles with large enough p will also justify the Born approximation.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|