Loop in Magnetic Field

A conducting circular loop made of wire of diameter d, resistivity ρ, and mass density ρ_m is falling from a great height h in a magnetic field with a component B_z = B₀(1+ kz), where k is some constant. The loop of diameter D is always parallel to the x-y plane. Disregarding air resistance, find the terminal velocity of the loop (see Figure 1.1).

Figure 1.1

SOLUTION

The magnetic force acting on the loop is proportional to its magnetic moment, which is proportional to the current flowing through the loop. The current I, in turn, is proportional to the rate of change of the magnetic flux through the loop, since I = ε_e/R, where ε_e is the electromotive force and R is the resistance of the loop. We have

The magnetic flux Φ in (1) is given by

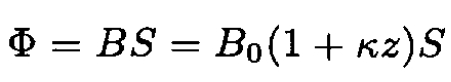(2)

where S is the area of the loop. From (1),

(3)

But dz/dt is the velocity of the loop. So the electromotive force increases with the velocity, and therefore the magnetic force F_m acting on the loop also increases with velocity, while the only other force, gravity, acting in the opposite direction, is constant. Therefore, the velocity will increase until F_m = mg From energy conservation, the work done by gravity during this stationary motion goes into the Joule heating of the loop:

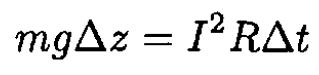(4)

But, since the velocity is constant,

(5)

where we substituted ε_e from (3) again using v = dz/dt. From (5), we can find

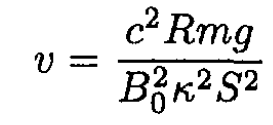(6)

Now, substituting

(7)

and

(8)

into (6), we obtain