بعض انواع المصفوفات:

نركز في هذا البند على بعض المصفوفات اتي لها شكل خاص. المصفوفات التي سندرسها هذه لها استخدامات مهمة في الجبر الخطي وبقية العلوم الرياضية.

تعريف (1-1):

المصفوفة القطرية هي المصفوفة المربعة التي جميع عناصرها خارج القطر الرئيسي تساوي صفر.

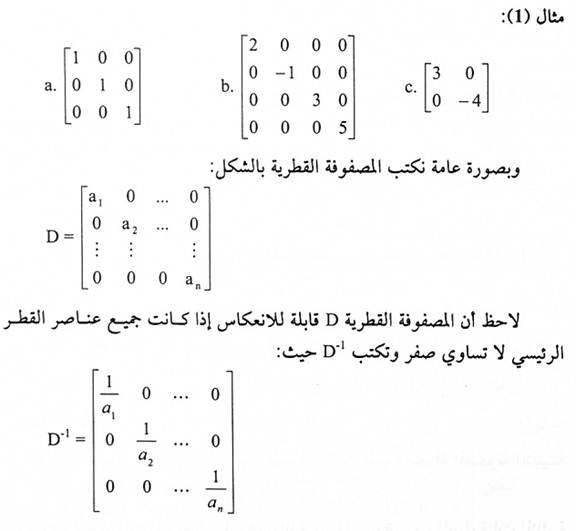
تعريف (1-2):

تسمى المصفوفة المربعة التي جميع عناصرها فوق القطر الرئيسي تساوي صفر بالمصفوفة المثلثية السفلى. اما التي جميع عناصرها أسفل القطر الرئيسي تساوي صفر فتسمى المصفوفة المثلثية العليا.

مثال (3):

مبرهنة (1-3):

1. منقولة المصفوفة المثلثية السفلى هي مصفوفة مثلثية عليا، ومنقولة المصفوفة المثلثية العليا هي مصفوفة مثلثية سفلي.

2. ضرب المصفوفات المثلثية السفلى هو مثلثية سفلى، وضرب المصفوفات المثلثية العليا هي مثلثية عليا.

3. المصفوفة المثلثية قابلة للانعكاس إذا وفقط إذا كانت عناصرها في القطر الرئيسي لا تساوي صفر.

4. معكوس المصفوفة المثلثية السفلى القابلة للانعكاس هي مثلثية سفلى، ومعكوس المصفوفة المثلثية العليا للانعكاس هي مثلثية عليا.

البرهان:

1. برهان هذا الجزء يمكن استنتاجه من حقيقة أن منقولة المصفوفة المربعة يمكن إنجازها بعكس العناصر الواقعة حول القطر الرئيسي.

2. نفرض أن A و B مصفوفات مثلثية سفلى، حيث [a_ij]A =  ، [b_ij] B =  و [C_ij] C = هي مصفوفة حاصل ضرب A و B

نبرهن أن C_ij = 0 لكل i<j من تعريف ضرب المصفوفات:

C_ij = a_ij b_ij + a_i2 b_2j + … + a_in b_nj (انظر تعريف ضرب المصفوفات).

نفرض أن i<j لذا فإن C_ij يمكن كتابتها بالشكل:

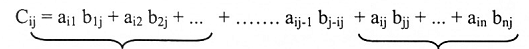
حدود فيها رقم صفوفه a أصغر من رقم أعمدة a               حدود فيها رقم صفوف b أصغر من رقم أعمدة b

ولما كانت B مثلثية سفلى فإن عوامل b في الجزء الأول تساوي صفر، كلك جميع عومل a في الجزء الثاني تساوي صفر لأن A

 مثلثية سفلى. عليه فإن C_ij = 0

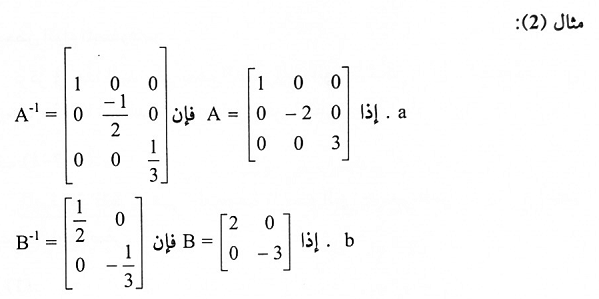
مثال(4):

لتكن                      

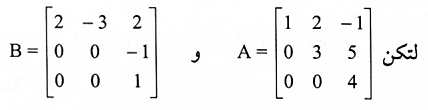
لاحظ أن A قابلة للانعكاس لأن جميع عناصر قطرها الرئيسي لا تساوي صفر بينما B غير قابلة للانعكاس.

تعريف (1-4):

المصفوفة المتناظرة  A  هي المصفوفة التي تساوي منقولتها أي، A^T = A

خواص المصفوفة المتناظرة:

لتكن A و B مصفوفتان متناظرتان وسعة كل منهما n x n فإن:

1. A^T متناظرة.

2. (A+B) متناظرة.

3. KA متناظرة (K ثابت) .

ملاحظة:

ضرب المصفوفات المتناظرة ليس ضرورياً أن يكون متناظراً.

مثال(5):

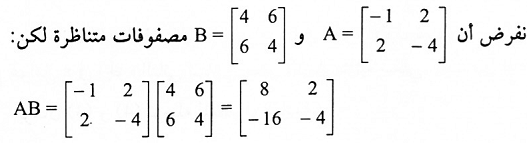
غير متناظرة.

(2) المصفوفة A^TA متناظرة لأن: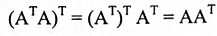        

وبنفس الطريقة AA^T.

مثال (6):

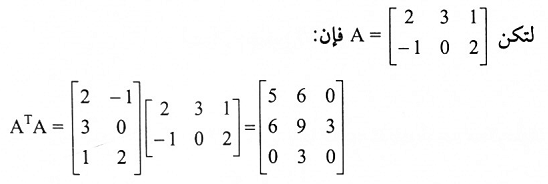
ومنها A^TA متناظرة.

مبرهنة (1-5):

1. إذا كانت A مصفوفة متناظرة وقابلة للانعكاس فإن A – 1 متناظرة.

2. إذا كانت A مصفوفة قابلة للانعكاس فإن A^TA و AA^T قابلتان للانعكاس.

البرهان:

1. نفرض A متناظرة وقابلة للانعكاس وحقيقة أن A^T = A نحصل على:

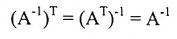
لذا A^-1 متناظرة.

2. بما أن A قابلة للانعكاس فإن A^T قابلة لانعكاس [مبرهنة 1-4-9] ، لذا فإن A^TA و AA^T قابلتان للانعكاس لأن كل منهما مضروب مصفوفتان قابلتان للانعكاس.