


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 6-2-2017
Date: 14-12-2015
Date: 26-1-2017
|
Entropy of Strings and Black Holes
The Bekenstein–Hawking entropy of black holes points to some kind of microphysical degrees of freedom, but it doesn't tell us what they are. A real theory of quantum gravity should tell us and also allow us to compute the entropy by quantum statistical mechanics, that is, counting microstates. In this lecture we will see to what extent string theory provides the microstructure and to what extent it enables us to compute black hole entropy microscopically.
String theory has many different kinds of black holes, some in 3 + 1 dimensions, some in higher dimensions. The black holes can be neutral or be charged with the various charges that string theory permits. We will see that for the entire range of such black holes, the statistical mechanics of strings allows us to compute the entropy up to numerical factors of order unity. In every case the results nontrivially agree with the Bekenstein–Hawking formula. What is more, in one or two cases in which the black holes are invariant under a large amount of supersymmetry the calculations can be refined and give the exact numerical coefficients. All of this is in cases where quantum field theory would give an infinite result.
Because string theory is not necessarily a 4-dimensional theory, it is worth exploring the connections between strings and black holes in any dimension. Let us begin with the formula for the entropy of a Schwarzschild black hole in an arbitrary number of dimensions. Call the number of spacetime dimensions D. The black hole metric found by solving Einstein's equation in D dimensions is given by
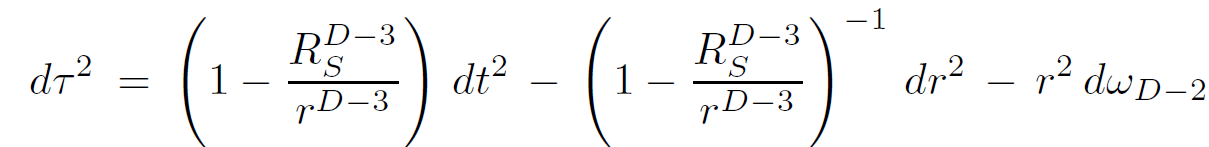 (1.1)
(1.1)
The horizon is defined by
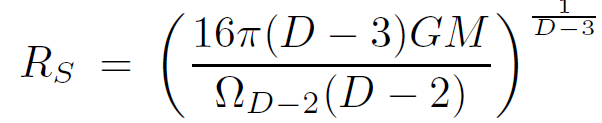 (1.2)
(1.2)
and its D-2 dimensional “area” is given by
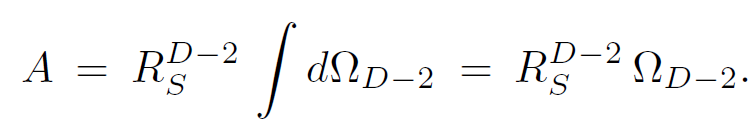 (1.3)
(1.3)
Finally, the entropy is given by
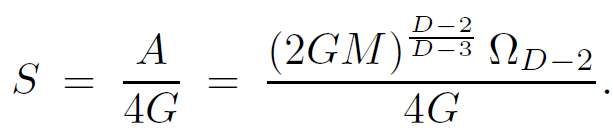 (1.4)
(1.4)
The entropy in equation 1.4 is what is required by black hole thermodynamics.
__________________________________________________________
Supplement: Schwarzschild geometry in D = d + 1 dimensions
To extend a static spherically symmetric geometry to D = d+1 dimensions, the metric can be assumed to be of the form
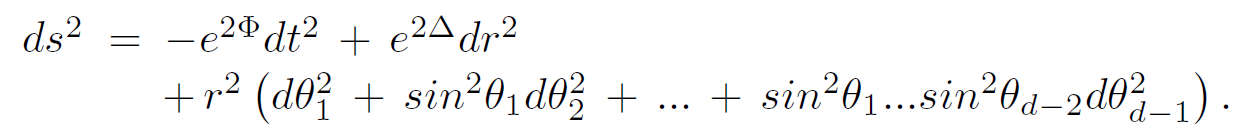 (1.5)
(1.5)
Using orthonormal coordinates, the 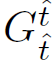 component of the Einstein tensor can be directly calculated to be of the form
component of the Einstein tensor can be directly calculated to be of the form
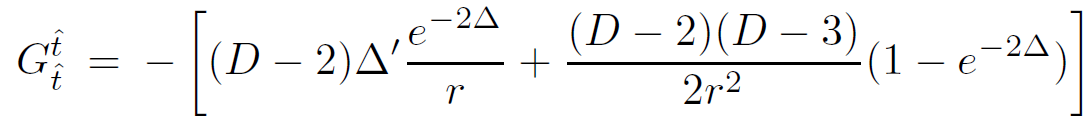 (1.6)
(1.6)
From Einstein's equation for ideal pressureless matter, 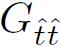 = κρ. This means
= κρ. This means
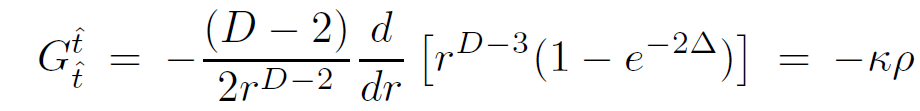 (1.7)
(1.7)
which can be solved to give
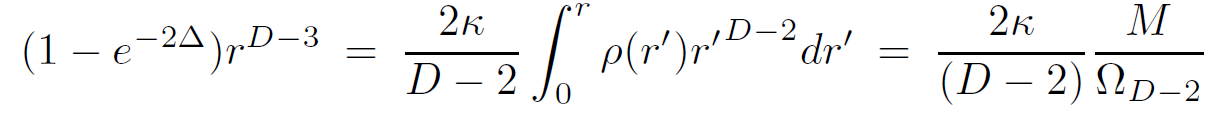 (1.8)
(1.8)
where the solid angle is given by ΩD−2 = 2π(D−1)/2/Γ((D−1)/2).The  component of the Einstein tensor satisfies
component of the Einstein tensor satisfies
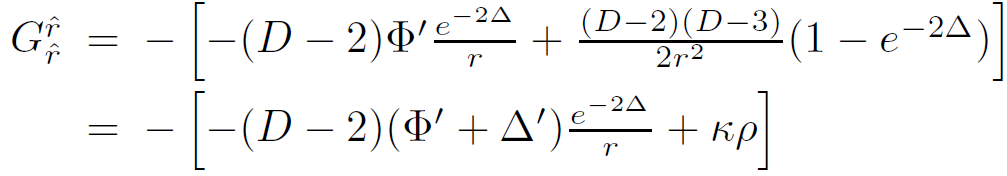 (1.9)
(1.9)
For pressureless matter in the exterior region (ρ = 0 = P), we can immediately conclude that Φ = −Δ. Defining the Schwarzschild radius RD−3S = 2κM/(D−2)ΩD−2 we obtain the form of the metric
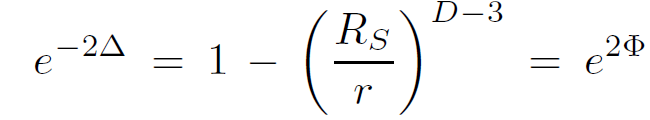 (1.10)
(1.10)
If we write F(r) ≡ e2Φ, a useful shortcut for calculating the solution to Einstein's equation 1.7 is to note its equivalence to the Newtonian Poisson equation in the exterior region
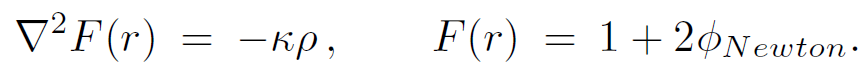 (1.11)
(1.11)
The Hawking temperature can be calculated by determining the dimensional factor between the Rindler time and Schwarzschild time. Near the horizon, the proper distance to the horizon is given by
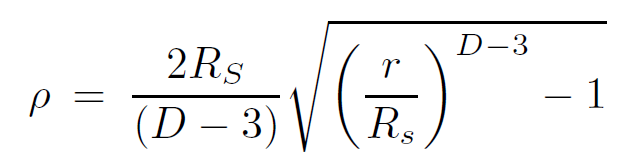 (1.12)
(1.12)
which gives the relation between Rindler time/temperature units and Schwarzschild time/temperature units
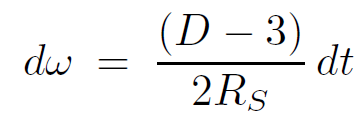 (1.13)
(1.13)
Thus, the Hawking temperature of the black hole is given by
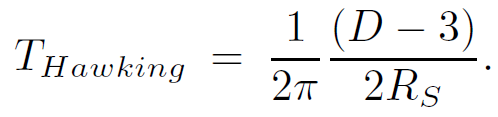 (1.14)
(1.14)
Using the first law of thermodynamics, the entropy can be directly calculated to be of the form
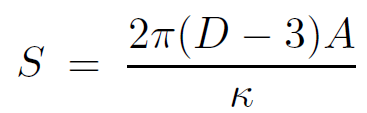 (1.15)
(1.15)
Substituting the form κ = 8π(D − 3)G for the gravitational coupling gives the previous results in D-dimensions.
All calculations of entropy in string theory make use of a well-known trick of quantum mechanics. The trick consists of identifying some kind of control parameter that can be adiabtically varied. In the process of adiabatic variation, energy levels are neither created nor destroyed. Thus if we can follow the system to a value of the control parameter where the system is tractable we can count the states easily even if the nature of the object changes during the variation. Basically we are using the quantum analog of the method of adiabatic invariants.
The trick in the string theory context is to vary the strength of the string coupling adiabatically until we arrive at a point where the gravitational forces are so weak that the black hole “morphs” into some more tractable object. Thus we begin with a black hole of mass Mo in a theory with string coupling go. Adiabatically varying a control parameter like go will cause a change in the black hole mass and other internal structural features. But such a variation will not alter its entropy. Entropy is an adiabatic invariant.
Let us imagine decreasing the string coupling g. What happens to the black hole as g tends to zero? The answer is obvious. It must turn into a collection of free strings. String theory has all kinds of non-perturbative objects, branes of various dimensionality such as membranes, D-branes, monopoles, and so on. But only the free strings have finite energy in the limit g → 0. Therefore a neutral black hole must evolve into a collection of free strings. A very massive black hole might evolve into a large number of low mass strings or, at the opposite extreme, a single very highly excited string.
Very highly excited free strings have an enormously rich spectrum. They can be thought of as a mass of tangled string that forms a time-varying random walk in space. Such random walking strings have a large entropy and can be studied statistically.
The entropy of a string of mass m can be calculated by returning to the light cone quantization of the previous lecture. For any eigenstate of the Hamiltonian with vanishing transverse momentum and unit P− the light cone energy is m2/2.
On the other hand the quantization of the string defines a 1+1 dimensional quantum field theory in which the (D-2) transverse coordinates Xi(σ) play the role of free scalar fields. The spatial coordinate of this field theory is σ1, and it runs from 0 to 2π.
The counting of the states of a free string is best done in the light cone version of the theory that we discussed in the last lecture. In order to describe the highly excited string spectrum, a formal light cone temperature T can be defined. Recall that the free string is described by means of a 1 + 1 dimensional quantum theory containing D − 2 fields Xi.
The entropy and energy of such a quantum field theory can be calculated by standard means. The leading contribution for large energy is (setting ℓs = 1)
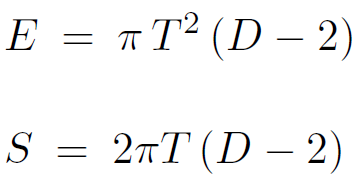 (1.16)
(1.16)
Using E = m2/2 and eliminating the temperature yields S = 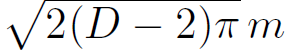 or, restoring the units
or, restoring the units
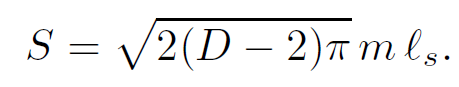 (1.17)
(1.17)
Subleading corrections can also be calculated to give
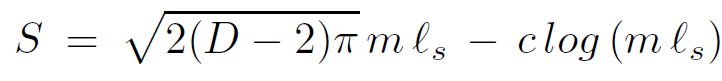 (1.18)
(1.18)
where c is a positive constant. The entropy is the log of the density of states. Therefore the number of states with mass m is
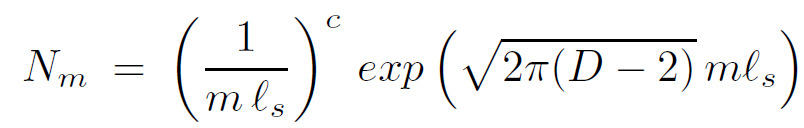 (1.19)
(1.19)
The formula 1.19 is correct for the simplest bosonic string, but similar formulae exist for the various versions of superstring theory.
Now let us compare the entropy of the single string with that of n strings, each carrying mass m/n . Call this entropy Sn(m).Then
Sn(m) = n S(m/n) (1.20)
or
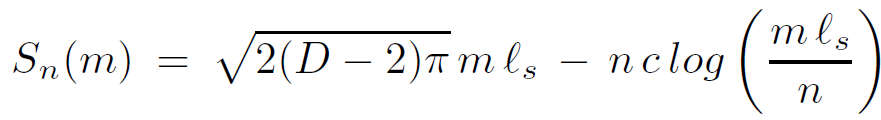 (1.21)
(1.21)
Obviously for large n the single string is favored. This is actually quite general. For a given total mass, the statistically most likely state in free string theory is a single excited string. Thus it is expected that when the string coupling goes to zero, most of the black hole states will evolve into a single excited string.
These observations allow us to estimate the entropy of a black hole. The assumptions are the following:
● A black hole evolves into a single string in the limit g → 0
● Adiabatically sending g to zero is an isentropic process; the entropy of the final string is the same as that of the black hole
● The entropy of a highly excited string of mass m is of order
S ∼ m ℓs (1.22)
● At some point as g → 0 the black hole will make a transition to a string. The point at which this happens is when the horizon radius is of the order of the string scale.
To understand this last assumption begin with a massive black hole. Gravity is clearly important and cannot be ignored. But no matter how massive the black hole is, as we decrease g a point will come where the gravitational constant is too weak to matter. That is the point where the black hole makes a transition and begins to act like a string. The string and Planck length scales are related by
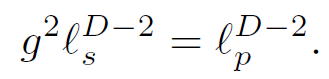 (1.23)
(1.23)
Evidently as g decreases the string length scale becomes increasingly big in Planck units. Eventually, at some value of the coupling that depends on the mass of the black hole, the string length will exceed the Schwarzschild radius of the black hole. This is the point at which the transition from black hole to string occurs. In what follows we will vary the g while keeping fixed the string length ℓs. This implies that the Planck length varies.
Let us begin with a black hole of mass Mo in a string theory with coupling constant go. The Schwarzschild radius is of order
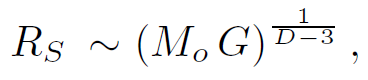 (1.24)
(1.24)
and using
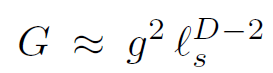 (1.25)
(1.25)
we find
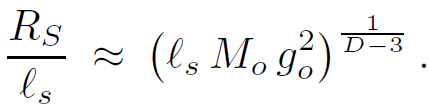 (1.26)
(1.26)
Thus for fixed go if the mass is large enough, the horizon radius will be much bigger than ℓs.
Now start to decrease g. In general the mass will vary during an adiabatic process. Let us call the g-dependent mass M(g). Note
M(go) = Mo (1.27)
The entropy of a Schwarzschild black hole (in any dimension) is a function of the dimensionless variable M ℓP. Thus, as long as the system remains a black hole,
M(g) ℓP = constant. (1.28)
Since ℓP ≈ ℓs g2/D−2 we can write equation 1.28 as
 (1.29)
(1.29)
Now as g → 0 the ratio of the g-dependent horizon radius to the string scale decreases. From equation 1.2 it becomes of order unity at
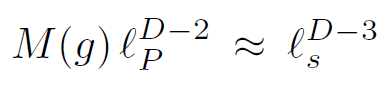 (1.30)
(1.30)
which can be written
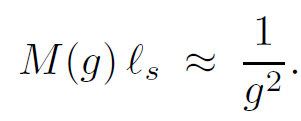 (15.0.31)
(15.0.31)
Combining equations 1.29 and 1.31 we find
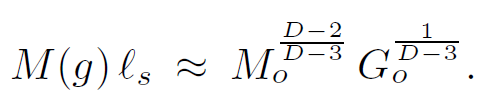 (1.32)
(1.32)
As we continue to decrease the coupling, the weakly coupled string mass will not change significantly. Thus we see that a black hole of mass Mo will evolve into a free string satisfying equation 1.32. But now we can compute the entropy of the free string. From equation 1.22 we find
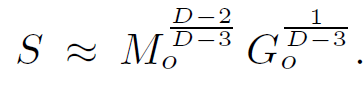 (1.33)
(1.33)
This is a very pleasing result in that it agrees with the Bekenstein–Hawking entropy in equation 1.4. However, in this calculation the entropy is calculated as the microscopic entropy of fundamental strings.
The evolution from black hole to string can be pictorially represented by starting with a large black hole. The stretched horizon is composed of a
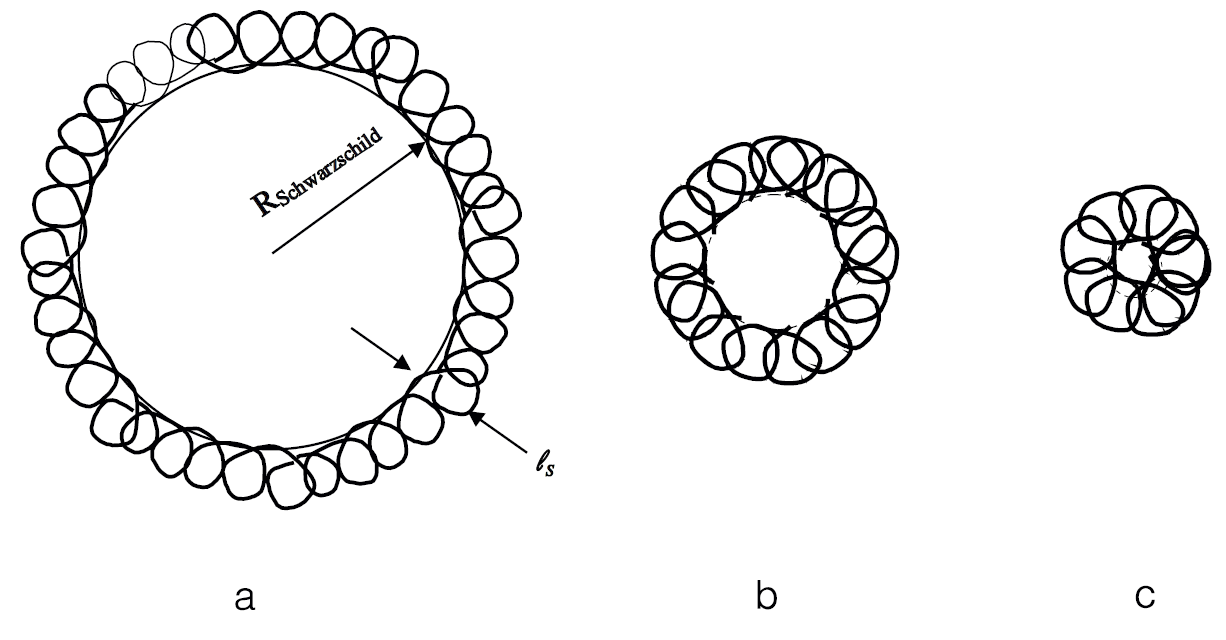
Fig. 1.1. Evolution from black hole to string. (a) A black hole with stringy stretched horizon smaller than Schwarzschild radius, (b) with stretched horizon and string scale comparable to radius scale, and (c) turned into a string.
stringy mass to a depth of ρ = ℓs as in the diagram Figure 1.1a. The area density of string is saturated at ∼ 1 /G. Another important property of the stretched horizon is its proper temperature. Since the proper temperature of a Rindler horizon is 1/2πρ , the temperature of the stringy mass will be
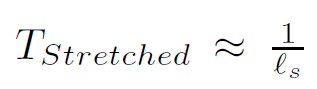
This temperature is close to the so called Hagedorn temperature, the maximum temperature that a string can achieve.
As the Schwarzschild radius is decreased (in string units), the area of the horizon decreases but the depth of the stretched horizon stays fixed as in Figure 1.1b. Finally the horizon radius is no larger than ℓs (Figure 1.1c) and the black hole turns into a string.
By now a wide variety of black holes that occur in string theory have been analyzed in this manner. The method is always the same. We adiabatically allow g to go to zero and identify the appropriate string configuration that the black hole evolves into.
A particularly interesting situation is that of charged extremal black holes which may be supersymmetric configurations of a supersymmetric theory. In this case the extremal black hole is absolutely stable and in addition, its mass is completely determined by supersymmetry. When this occurs there is no need to follow the mass of the black hole as g varies; the mass is fixed. Under these conditions the black hole can be compared directly to the corresponding weakly coupled string configuration and the entropy read off from the degeneracy of the string theory spectrum. In the cases where exact calculations are possible the charges carried by black holes are associated not with fundamental strings but D-branes. Nevertheless the principles are that same as those that we used to study the Schwarzschild black hole in D dimensions. The results in these more complicated examples are in precise agreement with the Hawking–Bekenstein entropy.
____________________________________________________________
Hagedorn Temperature Supplement
On general grounds, one can determine the density of states η for the various string modes m:
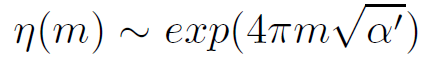
This allows the partition function to be written as
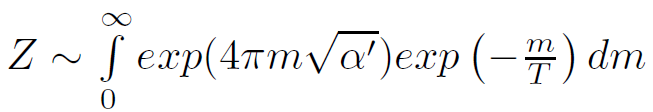
which diverges if the temperature T is greater than the Hagedorn temperature defined by
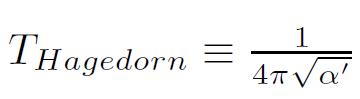
The Hagedorn temperature scales with the inverse string length
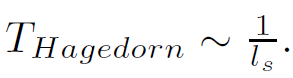
To get a feel for the scale of the Hagedorn temperature, recall the behavior of the entropy given by S∼ log(density of states).Using dimensional considerations, we have seen that the entropy of the string scales like
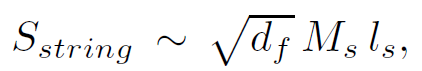
where df is the number of internal degrees of freedom available. Thus, the density of states behaves like
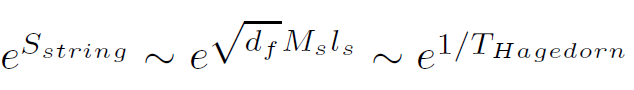
which gives the scale THagedorn∼ 1/l s. If one examines multi-string fluctuations as a function of temperature, the Hagedorn temperature is the “percolation” temperature for multiple strings fluctuations to coalesce into fluctuations of a single string as represented in Figure 1.2.
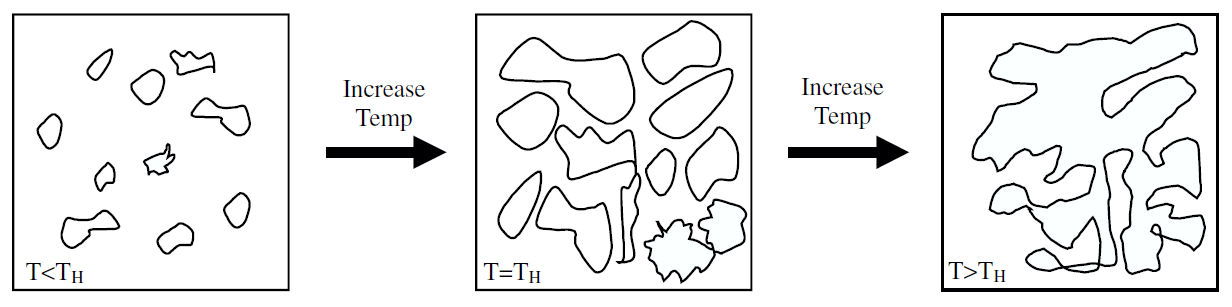
Fig. 1.2. String “percolation”.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|