


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-10-2015
Date: 14-10-2015
Date: 11-10-2015
|
The Indian numerals discussed in our article Indian numerals form the basis of the European number systems which are now widely used. However they were not transmitted directly from India to Europe but rather came first to the Arabic/Islamic peoples and from them to Europe. The story of this transmission is not, however, a simple one. The eastern and western parts of the Arabic world both saw separate developments of Indian numerals with relatively little interaction between the two. By the western part of the Arabic world we mean the regions comprising mainly North Africa and Spain. Transmission to Europe came through this western Arabic route, coming into Europe first through Spain.
There are other complications in the story, however, for it was not simply that the Arabs took over the Indian number system. Rather different number systems were used simultaneously in the Arabic world over a long period of time. For example there were at least three different types of arithmetic used in Arab countries in the eleventh century: a system derived from counting on the fingers with the numerals written entirely in words, this finger-reckoning arithmetic was the system used for by the business community; the sexagesimal system with numerals denoted by letters of the Arabic alphabet; and the arithmetic of the Indian numerals and fractions with the decimal place-value system.
The first sign that the Indian numerals were moving west comes from a source which predates the rise of the Arab nations. In 662 AD Severus Sebokht, a Nestorian bishop who lived in Keneshra on the Euphrates river, wrote:-
I will omit all discussion of the science of the Indians, ... , of their subtle discoveries in astronomy, discoveries that are more ingenious than those of the Greeks and the Babylonians, and of their valuable methods of calculation which surpass description. I wish only to say that this computation is done by means of nine signs. If those who believe, because they speak Greek, that they have arrived at the limits of science, would read the Indian texts, they would be convinced, even if a little late in the day, that there are others who know something of value.
This passage clearly indicates that knowledge of the Indian number system was known in lands soon to become part of the Arab world as early as the seventh century. The passage itself, of course, would certainly suggest that few people in that part of the world knew anything of the system. Severus Sebokht as a Christian bishop would have been interested in calculating the date of Easter (a problem to Christian churches for many hundreds of years). This may have encouraged him to find out about the astronomy works of the Indians and in these, of course, he would find the arithmetic of the nine symbols.
By 776 AD the Arab empire was beginning to take shape and we have another reference to the transmission of Indian numerals. We quote from a work of al-Qifti Chronology of the scholars written around the end the 12th century but quoting much earlier sources:-
... a person from India presented himself before the Caliph al-Mansur in the year [ 776 AD] who was well versed in the siddhanta method of calculation related to the movment of the heavenly bodies, and having ways of calculating equations based on the half-chord [essentially the sine] calculated in half-degrees ... This is all contained in a work ... from which he claimed to have taken the half-chord calculated for one minute. Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arabs a solid base for calculating the movements of the planets ...
Now in [1] (where a longer quote is given) Ifrah tries to determine which Indian work is referred to. He concludes that the work was most likely to have been Brahmagupta's Brahmasphutasiddhanta (The Opening of the Universe) which was written in 628. Irrespective of whether Ifrah is right, since all Indian texts after Aryabhata I's Aryabhatiya used the Indian number system of the nine signs, certainly from this time the Arabs had a translation into Arabic of a text written in the Indian number system.
It is often claimed that the first Arabic text written to explain the Indian number system was written by al-Khwarizmi. However there are difficulties here which many authors tend to ignore. The Arabic text is lost but a twelfth century Latin translation, Algoritmi de numero Indorum (in English Al-Khwarizmi on the Hindu Art of Reckoning) gave rise to the word algorithm deriving from his name in the title. Unfortunately the Latin translation is known to be much changed from al-Khwarizmi's original text (of which even the title is unknown). The Latin text certainly describes the Indian place-value system of numerals based on 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. The first use of zero as a place holder in positional base notation is considered by some to be due to al-Khwarizmi in this work. The difficulty which arises is that al-Baghdadi refers to the Arabic original which, contrary to what was originally thought, seems not to be a work on Indian numerals but rather a work on finger counting methods. This becomes clear from the references by al-Baghdadi to the lost work. However the numerous references to al-Khwarizmi's book on the Indian nine symbols must mean that he did write such a work. Some degree of mystery still remains.
At first the Indian methods were used by the Arabs with a dust board. In fact in the western part of the Arabic world the Indian numerals came to be known as Guba (or Gubar or Ghubar) numerals from the Arabic word meaning "dust". A dust board was used because the arithmetical methods required the moving of numbers around in the calculation and rubbing some out some of them as the calculation proceeded. The dust board allowed this in the same sort of way that one can use a blackboard, chalk and a blackboard eraser. Any student who has attended lectures where the lecturer continually changes and replaces parts of the mathematics as the demonstration progresses will understand the disadvantage of the dust board!
Around the middle of the tenth century al-Uqlidisi wrote Kitab al-fusul fi al-hisab al-Hindi which is the earliest surviving book that presents the Indian system. In it al-Uqlidisi argues that the system is of practical value:-
Most arithmeticians are obliged to use it in their work: since it is easy and immediate, requires little memorisation, provides quick answers, demands little thought ... Therefore, we say that it is a science and practice that requires a tool, such as a writer, an artisan, a knight needs to conduct their affairs; since if the artisan has difficulty in finding what he needs for his trade, he will never succeed; to grasp it there is no difficulty, impossibility or preparation.
In the fourth part of this book al-Uqlidisi showed how to modify the methods of calculating with Indian symbols, which had required a dust board, to methods which could be carried out with pen and paper. Certainly the fact that the Indian system required a dust board had been one of the main obstacles to its acceptance. For example As-Suli, after praising the Indian system for its great simplicity, wrote in the first half of the tenth century:-
Official scribes nevertheless avoid using [the Indian system] because it requires equipment [like a dust board] and they consider that a system that requires nothing but the members of the body is more secure and more fitting to the dignity of a leader.
Al-Uqlidisi's work is therefore important in attempting to remove one of the obstacles to acceptance of the Indian nine symbols. It is also historically important as it is the earliest known text offering a direct treatment of decimal fractions.
Despite many scholars finding calculating with Indian symbols helpful in their work, the business community continued to use their finger arithmetic throughout the tenth century. Abu'l-Wafa, who was himself an expert in the use of Indian numerals, nevertheless wrote a text on how to use finger-reckoning arithmetic since this was the system used by the business community and teaching material aimed at these people had to be written using the appropriate system. Let us give a little information about the Arab letter numerals which are contained in Abu'l-Wafa's work.
The numbers were represented by letters but not in the dictionary order. The system was known as huruf al jumal which meant "letters for calculating" and also sometimes as abjad which is just the first four numbers (1 = a, 2 = b, j = 3, d = 4). The numbers from 1 to 9 were represented by letters, then the numbers 10, 20, 30, ..., 90 by the next nine letters (10 = y, 20 = k, 30 = l, 40 = m, ...), then 100, 200, 300, ... , 900 by the next letters (100 = q, 200 = r, 300 = sh, 400 = ta, ...). There were 28 Arabic letters and so one was left over which was used to represent 1000.
Arabic astronomers used a base 60 version of Arabic letter system. Although Arabic is written from right to left, we shall give an example writing in the left to right style that we use in writing English. A number, say 43° 21' 14", would have been written as "mj ka yd" in this base 60 version of the "abjad" letters for calculating.
A contemporary of al-Baghdadi, writing near the beginning of the eleventh century, was ibn Sina (better known in the West as Avicenna). We know many details of his life for he wrote an autobiography. Certainly ibn Sina was a remarkable child, with a memory and an ability to learn which amazed the scholars who met in his father's home. A group of scholars from Egypt came to his father's house in about 997 when ibn Sina was ten years old and they taught him Indian arithmetic. He also tells of being taught Indian calculation and algebra by a seller of vegetables. All this shows that by the beginning of the eleventh century calculation with the Indian symbols was fairly widespread and, quite significantly, was know to a vegetable trader.
What of the numerals themselves. We have seen in the article Indian numerals that the form of the numerals themselves varied in different regions and changed over time. Exactly the same happened in the Arabic world.
Here is an example of an early form of Indian numerals being used in the eastern part of the Arabic empire. It comes from a work of al-Sijzi, not an original work by him but rather the work of another mathematician which al-Sijzi copied at Shiraz and dated his copy 969.

The numerals from al-Sizji's treatise of 969
The numerals had changed their form somewhat 100 years later when this copy of one of al-Biruni's astronomical texts was made. Here are the numerals as they appear in a 1082 copy.
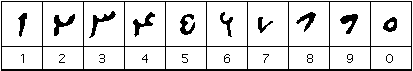
The numerals from al-Biruni's treatise copied in 1082
In fact a closer look will show that between 969 and 1082 the biggest change in the numerals was the fact that the 2 and the 3 have been rotated through 90°. There is a reason for this change which came about due to the way that scribes wrote, for they wrote on a scroll which they wound from right to left across their bodies as they sat cross-legged. The scribes therefore, instead of writing from right to left (the standard way that Arabic was written) wrote in lines from top to bottom. The script was rotated when the scroll was read and the characters when then in the correct orientation.

Here is an example of how the text was written
Perhaps because scribes did not have much experience at writing Indian numerals, they wrote 2 and 3 the correct way round instead of writing them rotated by 90° so that they would appear correctly when the scroll was rotated to be read.
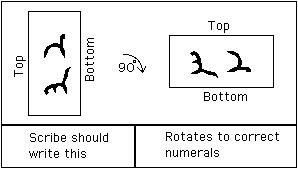
Here is an example of what the scribe should write
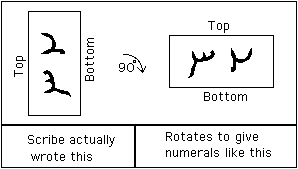
and here is what the scribe actually wrote
The form of the numerals in the west of the Arabic empire look more familiar to those using European numerals today which is not surprising since it is from these numerals that the Indian number system reach Europe.
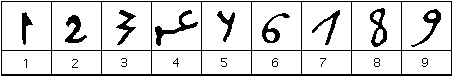
al-Banna al-Marrakushi's form of the numerals
He gave this form of the numerals in his practical arithmetic book written around the beginning of the fourteenth century. He lived most of his life in Morocco which was in close contact with al-Andalus, or Andalusia, which was the Arab controlled region in the south of Spain.
The first surviving example of the Indian numerals in a document in Europe was, however, long before the time of al-Banna. The numerals appear in the Codex Vigilanus copied by a monk in Spain in 976. However the main part of Europe was not ready at this time to accept new ideas of any kind. Acceptance was slow, even as late as the fifteenth century when European mathematics began its rapid development which continues today. We will not examine the many contributions to bringing the Indian number system to Europe in this article but we will end with just one example which, however, is a very important one.Fibonacci writes in his famous book Liber abaci published in Pisa in 1202:-
When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it, for whatever was studied by the art in Egypt, Syria, Greece, Sicily and Provence, in all its various forms.
______________________________________________________________________________________________



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|