


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات The dominance relation on a set of points in Euclidean 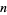 -space is the intersection of the
-space is the intersection of the 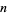 coordinate-wise orderings. A point
coordinate-wise orderings. A point 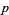 dominates a point
dominates a point 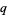 provided that every coordinate of
provided that every coordinate of 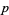 is at least as large as the corresponding coordinate of
is at least as large as the corresponding coordinate of 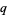 .
.
A partition 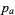 dominates a partition
dominates a partition 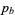 if, for all
if, for all 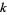 , the sum of the
, the sum of the 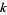 largest parts of
largest parts of 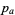 is
is 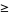 the sum of the
the sum of the 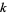 largest parts of
largest parts of 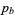 . For example, for
. For example, for 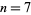 ,
, 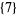 dominates all other partitions, while
dominates all other partitions, while 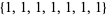 is dominated by all others. In contrast,
is dominated by all others. In contrast, 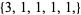 and
and 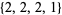 do not dominate each other (Skiena 1990, p. 52).
do not dominate each other (Skiena 1990, p. 52).
The dominance orders in 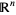 are precisely the partially ordered sets of dimension at most
are precisely the partially ordered sets of dimension at most 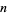 .
.
REFERENCES:
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, 1990.
Stanton, D. and White, D. Constructive Combinatorics. New York: Springer-Verlag, 1986.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|