


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-12-2021
Date: 31-12-2021
Date: 14-2-2017
|
An algebra 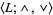 is called a lattice if
is called a lattice if 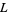 is a nonempty set,
is a nonempty set, 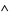 and
and 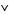 are binary operations on
are binary operations on 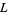 , both
, both 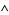 and
and 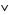 are idempotent, commutative, and associative, and they satisfy the absorption law. The study of lattices is called lattice theory.
are idempotent, commutative, and associative, and they satisfy the absorption law. The study of lattices is called lattice theory.
Note that this type of lattice is distinct from the regular array of points known as a point lattice (or informally as a mesh or grid). While every point lattice is a lattice under the ordering inherited from the plane, many lattices are not point lattices.
Lattices offer a natural way to formalize and study the ordering of objects using a general concept known as the partially ordered set. A lattice as an algebra is equivalent to a lattice as a partially ordered set (Grätzer 1971, p. 6) since
1. Let the partially ordered set 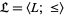 be a lattice. Set
be a lattice. Set 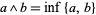 and
and 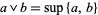 . Then the algebra
. Then the algebra 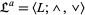 is a lattice.
is a lattice.
2. Let the algebra 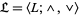 be a lattice. Set
be a lattice. Set 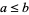 iff
iff 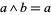 . Then
. Then 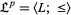 is a partially ordered set, and the partially ordered set
is a partially ordered set, and the partially ordered set 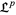 is a lattice.
is a lattice.
3. Let the partially ordered set 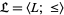 be a lattice. Then
be a lattice. Then 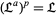 .
.
4. Let the algebra 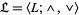 be a lattice. Then
be a lattice. Then 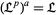 .
.
The following inequalities hold for any lattice:
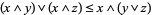 |
(1) |
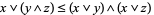 |
(2) |
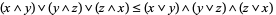 |
(3) |
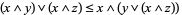 |
(4) |
(Grätzer 1971, p. 35). The first three are the distributive inequalities, and the last is the modular identity.
A lattice 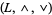 can be obtained from a lattice-ordered poset
can be obtained from a lattice-ordered poset 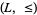 by defining
by defining 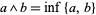 and
and 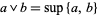 for any
for any 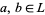 . Also, from a lattice
. Also, from a lattice 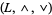 , one may obtain a lattice-ordered set
, one may obtain a lattice-ordered set 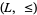 by setting
by setting 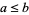 in
in 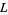 if and only if
if and only if 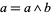 . One obtains the same lattice-ordered set
. One obtains the same lattice-ordered set 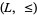 from the given lattice by setting
from the given lattice by setting 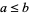 in
in 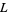 if and only if
if and only if 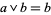 . (In other words, one may prove that for any lattice,
. (In other words, one may prove that for any lattice, 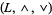 , and for any two members
, and for any two members 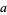 and
and 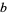 of
of 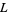 ,
, 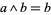 if and only if
if and only if 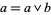 .)
.)
REFERENCES:
Grätzer, G. Lattice Theory: First Concepts and Distributive Lattices. San Francisco, CA: W. H. Freeman, 1971.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|