


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 15-12-2021
التاريخ: 6-1-2022
التاريخ: 14-12-2021
التاريخ: 9-12-2021
|
الحجم الحرج Critical Size للمفاعلات المتجانسة
عندما يكون المفاعل حرجاً فإن حالة الاستقرار تتحقق. ولتحديد حجم المفاعل ينبغي أولاً وضع تعبير مناسب لحد المصدر (S). فإن النيوترونات تنتج أساساً عن الانشطار وبالتالي فإنه عندما يتم امتصاص نيوترون واحد في الوقود فإن ذلك ينتج عنه تولد عدد من النيوترونات قدره ∞K، فإذا كان معدل امتصاص النيوترونات/ وحدة الحجوم يساوي ∅ a∑ فإن:
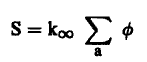
وبالتعويض في معادلة الاتية:
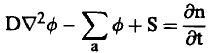
ينتج أن:
(1) ...................
وهذه هي معادلة المفاعل الحرج:
و بإعادة ترتيب الحدود نجد أن :
(2)...........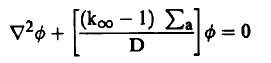
ومن معادلة الاتية:

نجد أن:
(3).............
لاحظ أن هذه المعادلة صحيحة عندما 1 = Keff أي 1= P ∞K ولاحظ أيضاً أننا افترضنا أن لدينا مجموعة من النيوترونات وحيدة الطاقة. ومن ثم تعرف هذه المعادلة بمعادلة المجموعة الواحدة الحرجة: The One - Group Critical Equation. يمكن الآن كتابة هذه المعادلة على الصورة:
(4).........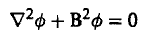
حيث تعرف B بانحناء المنظومة Buckling» of the suystem» وذلك لأنها تعبر عن درجة انحناء التوزيع المكاني Spatial Distribution لفيض النيوترونات.
وفي حالة المفاعل المكشوف Bare Reactor أو المفاعل بدون العاكس نجد أن العلاقة السابقة تعطي شرط الحروجة لمثل هذا المفاعل وذا المجموعة الواحدة، ومن ثم فإننا نستعيض عن B بالانحناء الحرج (Bc) ومن معادلتي (3، 4) فإن:
(5) ............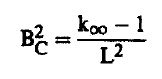
وتبين هذه المعادلة أنه يمكن تعيين قيمة Bc بمعرفة كل من ∞KL2, واللتين تعبران عن منظومة الوقود - المهدئ . ولهذا تسمى هذه القيمة أحياناً بانحناء المواد Material Bucking.
باستخدام المعادلة السابقة نجد أن:
(6) ............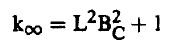
ومن معادلة الاتية:
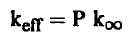
وباستخدام شرط الحروجة Keff = 1 نجد أن إحتمال عدم التسرب P يعطي بالعلاقة:
(7) ..................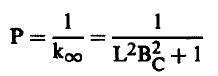
ومن معادلة (5) يمكن كتابة شرط الحروجة (بعد إجراء بعض التعديلات في المعادلة) على الصورة:
(8) ............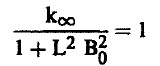
ولتحديد الحجم الحرج للمفاعل فإن علينا أن نحل معادلة (4) لتعيين قيمة B2 وذلك لشكل هندسي معين للمفاعل وعند شرط حد معين ومن ثم تعيين إبعاد المفاعل.
أما إذا أخذنا في الاعتبار النيوترونات السريعة ايضاً فإننا نتحدث عن معادلة المجموعتين الحرجة Tow - Group Critical Equation. حيث تعتبر هنا أن النيوترونات إما أن تكون سريعة أو حرارية. وسوف تعاني النيوترونات السريعة عدة تصادمات قبل أن تتباطاً وتصبح حرارية، مروراً ببعض احتمالات الامتصاص أيضاً. كما وأن البعض من هده النيوترونات السريعة قد يتمكن من التسرب خارج المنظومة أثناء تباطوها ومن ثم يمكن أخذ كل هذه الحالات في الاعتبار لتمكن في النهاية من كتابة معادلة حروجة أقرب إلى الواقع.
يمكننا كتابة معادلتين كالمعادلة (4) إحداهما خاصة بمجموعة النيوترونات الحرارية، والأخرى خاصة بالنيوترونات السريعة، وينتج أن:
(9)....... 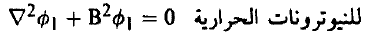
(10).....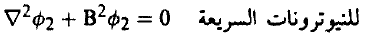
وكما فعلنا آنفاً فإننا يمكن أن نستنتج أن :
(11).............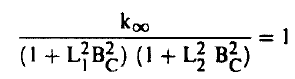
حيث Bc هي الانحناء في توزيع فيض النيوترونات الحرارية والسريعة.
L2, L1 طول الانتشار للنيوترونات الحرارية والسريعة، على الترتيب.
وهناك طريقة أخرى تتبع لدراسة توزيع الفيض تسمى طريقة عمر الانتشار Age - Diffusion Methodحيث يعرف فيها المتغير ((Eτ حيث:
(12) ............
حيث 0E طاقة النيوترونات عند خروجها من المصدر.
S∑ مساحة مقطع التشتت الماكروسكوبي .
ξ المتوسط اللوغاريتمي لمعدل فقد الطاقة/تصادم أو Average collision per logarithmic energy decrement.
ويعطي بالعلاقة:
(13) ............
حيث E2, E1 طاقتي النيوترونات قبل وبعد التصادم، على الترتيب.
يمكن الآن استبدال L21 في معادلة (11) بالمتغير (τ) وينتج ان:
(14)...........
كما وتصبح معادلة (4) على الصورة التالية:
(15) ........
ومنها ينتج أن:
حيث τth ترمز إلى عمر الاتثار للنيوترون عندما يصبح نيوترون حراري.
وتعرف هذه المعادلة بمعادلة عمر الانتشار الحرجة age - diffusion critical equation.
لاحظ أن وحدات τ هي مربع المسافة. كما وأن τ لها علاقة بمتوسط مربع المسافة المقطوعة بواسطة النيوترونات أثناء عملية تباطؤها. وبالتالي يمكن تعريف طول التباطؤ Slowing Down Length على أنه يساوي الجذر التربيعي للعمر (τ) . كما ويمكن تعريف الكمية M التي تعرف بطول الارتحال Migration Length حيث:
(16)..........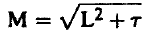
ومنها يمكن تعريف مساحة الارتحالMigration Area (M) حيث:
(17)..........
نبين في الجدول (1) قيم عمر (Age) نيوترونات حرارية عند درجة C20o ناتجة من مصدر انشطار نووي. وذلك لمهدئات مختلفة.
الجدول (1)

كما نبين في الجدول (2) طول الارتحال للنيوترونات الحرارية وطول الانتشار وطول التباطؤ. وذلك للمهدئات السابقة في الجدول (1).
الجدول (2) اطوال الارتحال والانتشار والتباطؤ للنيوترونات الحرارية في مهدئات مختلفة،

كما ونبين في الجدول (4) مساحات مقاطع النيوترونات الحرارية ذات سرعة تساوي m/s 2200 (مقدرة بالبارن) في مواد مختلفة ذات علاقة بتصاميم المفاعلات النووية.
الجدول (3)
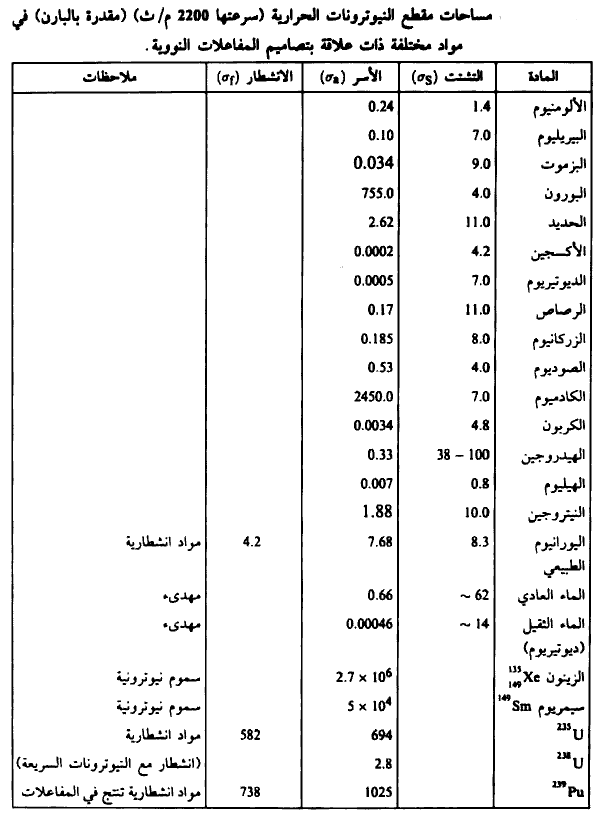
ولغرض استيفاء البيانات نبين في الشكل (1) مساحة مقطع الانشطار في اليورانيوم - 235 ومساحتي المقطعين الكليين في اليورانيوم - 235 و238.

الشكل (1)
يمكن الآن تعيين إبعاد الحجم الحرج لشكل هندسي معين للمفاعل. ووفق شروط حد معين. وذلك بإيجاد حل عام لمعادلة (4). وسوف نعتبر الشكل الكروي كمثال نطبق عليه الحل بينما لن تختلف حلول باقي الأشكال الهندسية عن هذا الحل. يعطي الحل العام للفيض (r) ∅ على بعد قدره (r) من نقطة لأصل بالعلاقة:

حيث B, A ثوابت يمكن تعيينها، ومن الشروط العملية نجد أن الفيض يأخذ قيمة محددة عند نقطة الأصل (0 = r) فإن:
(18)..............
ومن الشروط الابتدائية وباعتبار أن لدينا مفاعلاً كروياً قطره R فإنه عندما r = R ينعدم الفيض (مع فرض زيادة صغيرة للفيض خارج R) فإن:
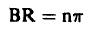
اي ان:
(19)........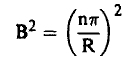
حيث ... 1,2,3 = n.
وبأخذ القيمة العملية (1 = n) وعندما تساوي R نصف القطر الحرج (Rc) وتساوي (Bc) فإن:
(20) ........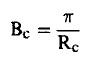
وبالتعويض في معادلة (18) من معادلة (20) لتعيين الفيض في المفاعل الحرج ينتج أن:
(21) .............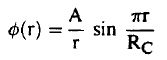
أما الثابت A فيمكن تعيينه عملياً بقياس مستوى القدرة في المفاعل.
يبين الشكل (2) أشكالاً هندسية لقلوب مفاعلات نووية مختلفة ونبين

الشكل (2)
في الجدول (4) ملخصاً للنتائج التي يمكن التحصل عليها لثلاثة أشكال للمفاعلات والتي نبين الانحناء وتوزيع الفيض الحرج للنيوترونات في المفاعل وكذلك أقل حجم حرج للمفاعل في كل حالة. لاحظ هنا أن الحجم الحرج للمفاعل الكروي هو أقل حجم حرج لأي شكل هندسي آخر وذلك لأن أدنى تسرب يحدث للشكل الذي تكون نسبة مساحة السطح إلى الحجم أقل ما يمكن ولا يتأتى ذلك إلا للكرة حيث تتمتع بأقل نسبة بين مساحة السطح إلى الحجم. وبالتالي فإن أقل حجم حرج يتمتع به الشكل الكروي.
الجدول (4)




|
|
|
|
هل يمكن أن تكون الطماطم مفتاح الوقاية من السرطان؟
|
|
|
|
|
|
|
اكتشاف عرائس"غريبة" عمرها 2400 عام على قمة هرم بالسلفادور
|
|
|
|
|
|
|
جامعة الكفيل تقيم ندوة علمية عن الاعتماد الأكاديمي في جامعة جابر بن حيّان
|
|
|