


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-12-2021
Date: 14-12-2021
Date: 2-12-2021
|
Legendre-Gauss quadrature is a numerical integration method also called "the" Gaussian quadrature or Legendre quadrature. A Gaussian quadrature over the interval ![[-1,1]](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/Inline1.gif) with weighting function
with weighting function 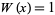 . The abscissas for quadrature order
. The abscissas for quadrature order 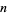 are given by the roots of the Legendre polynomials
are given by the roots of the Legendre polynomials 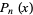 , which occur symmetrically about 0. The weights are
, which occur symmetrically about 0. The weights are
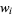 |
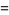 |
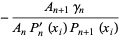 |
(1) |
 |
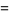 |
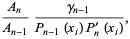 |
(2) |
where 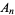 is the coefficient of
is the coefficient of 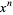 in
in 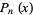 . For Legendre polynomials,
. For Legendre polynomials,
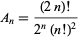 |
(3) |
(Hildebrand 1956, p. 323), so
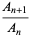 |
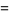 |
![([2(n+1)]!)/(2^(n+1)[(n+1)!]^2)(2^n(n!)^2)/((2n)!)](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/Inline16.gif) |
(4) |
 |
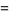 |
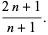 |
(5) |
Additionally,
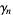 |
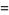 |
![int_(-1)^1[P_n(x)]^2dx](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/Inline22.gif) |
(6) |
 |
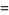 |
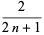 |
(7) |
(Hildebrand 1956, p. 324), so
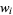 |
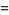 |
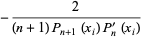 |
(8) |
 |
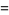 |
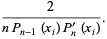 |
(9) |
Using the recurrence relation
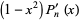 |
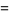 |
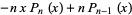 |
(10) |
 |
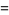 |
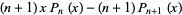 |
(11) |
(correcting Hildebrand 1956, p. 324) gives
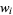 |
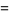 |
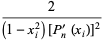 |
(12) |
 |
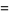 |
![(2(1-x_i^2))/((n+1)^2[P_(n+1)(x_i)]^2)](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/Inline43.gif) |
(13) |
(Hildebrand 1956, p. 324).
The weights 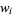 satisfy
satisfy
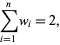 |
(14) |
which follows from the identity
![sum_(nu=1)^n(1-x_nu^2)/((n+1)^2[P_(n+1)(x_nu)]^2)=1.](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/NumberedEquation3.gif) |
(15) |
The error term is
![E=(2^(2n+1)(n!)^4)/((2n+1)[(2n)!]^3)f^((2n))(xi).](https://mathworld.wolfram.com/images/equations/Legendre-GaussQuadrature/NumberedEquation4.gif) |
(16) |
Beyer (1987) gives a table of abscissas and weights up to 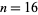 , and Chandrasekhar (1960) up to
, and Chandrasekhar (1960) up to 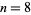 for
for 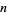 even.
even.
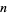 |
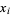 |
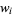 |
| 2 | 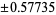 |
1.000000 |
| 3 | 0 | 0.888889 |
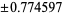 |
0.555556 | |
| 4 | 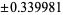 |
0.652145 |
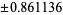 |
0.347855 | |
| 5 | 0 | 0.568889 |
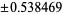 |
0.478629 | |
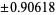 |
0.236927 |
The exact abscissas are given in the table below.
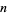 |
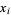 |
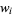 |
| 2 | 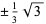 |
1 |
| 3 | 0 | 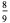 |
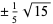 |
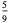 |
|
| 4 | 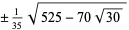 |
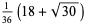 |
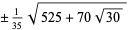 |
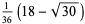 |
|
| 5 | 0 | 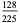 |
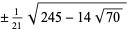 |
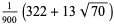 |
|
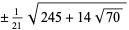 |
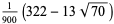 |
The abscissas for order 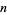 quadrature are roots of the Legendre polynomial
quadrature are roots of the Legendre polynomial 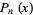 , meaning they are algebraic numbers of degrees 1, 2, 2, 4, 4, 6, 6, 8, 8, 10, 10, 12, ..., which is equal to
, meaning they are algebraic numbers of degrees 1, 2, 2, 4, 4, 6, 6, 8, 8, 10, 10, 12, ..., which is equal to 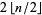 for
for 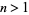 (OEIS A052928).
(OEIS A052928).
Similarly, the weights for order 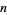 quadrature can be expressed as the roots of polynomials of degree 1, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, ..., which is equal to
quadrature can be expressed as the roots of polynomials of degree 1, 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, ..., which is equal to 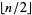 for
for 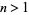 (OEIS A008619). The triangle of polynomials whose roots determine the weights is
(OEIS A008619). The triangle of polynomials whose roots determine the weights is
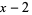 |
(17) |
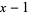 |
(18) |
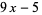 |
(19) |
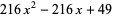 |
(20) |
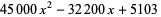 |
(21) |
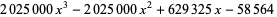 |
(22) |
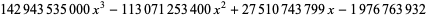 |
(23) |
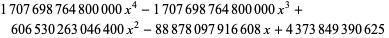 |
(24) |
REFERENCES:
Abbott, P. "Tricks of the Trade: Legendre-Gauss Quadrature." Mathematica J. 9, 689-691, 2005.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 462-463, 1987.
Chandrasekhar, S. Radiative Transfer. New York: Dover, pp. 56-62, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 323-325, 1956.
Sloane, N. J. A. Sequences A008619, A052928, and A112734 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|