Secant Method

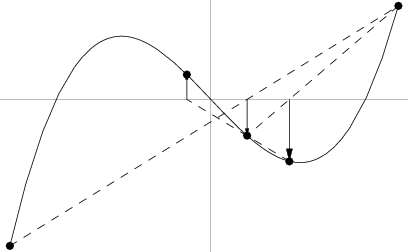
A root-finding algorithm which assumes a function to be approximately linear in the region of interest. Each improvement is taken as the point where the approximating line crosses the axis. The secant method retains only the most recent estimate, so the root does not necessarily remain bracketed. The secant method is implemented in the Wolfram Language as the undocumented option Method -> Secant in FindRoot[eqn, 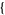x, x0, x1].

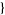When the algorithm does converge, its order of convergence is

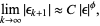(1)

where 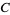 is a constant and  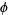is the golden ratio.

(2)

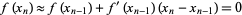(3)

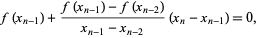(4)

so

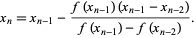(5)

The secant method can be implemented in the Wolfram Language as

  SecantMethodList[f_, {x_, x0_, x1_}, n_] :=
    NestList[Last[#] - {0, (Function[x, f][Last[#]]*
      Subtract @@ #)/Subtract @@
      Function[x, f] /@ #}&, {x0, x1}, n]

REFERENCES:

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Secant Method, False Position Method, and Ridders' Method." §9.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 347-352, 1992.