


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-5-2021
Date: 24-5-2021
Date: 5-6-2021
|
The compact-open topology is a common topology used on function spaces. Suppose 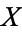 and
and 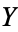 are topological spaces and
are topological spaces and 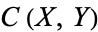 is the set of continuous maps from
is the set of continuous maps from 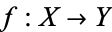 . The compact-open topology on
. The compact-open topology on 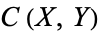 is generated by subsets of the following form,
is generated by subsets of the following form,
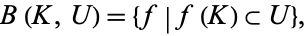 |
(1) |
where 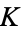 is compact in
is compact in 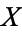 and
and 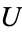 is open in
is open in 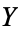 . (Hence the terminology "compact-open.") It is important to note that these sets are not closed under intersection, and do not form a topological basis. Instead, the sets
. (Hence the terminology "compact-open.") It is important to note that these sets are not closed under intersection, and do not form a topological basis. Instead, the sets 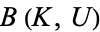 form a subbasis for the compact-open topology. That is, the open sets in the compact-open topology are the arbitrary unions of finite intersections of
form a subbasis for the compact-open topology. That is, the open sets in the compact-open topology are the arbitrary unions of finite intersections of 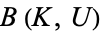 .
.
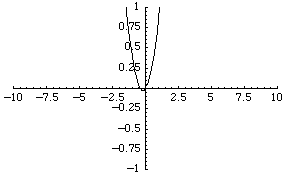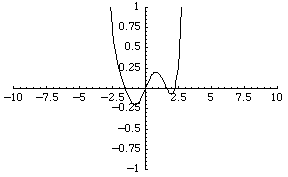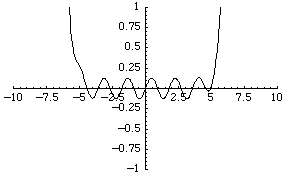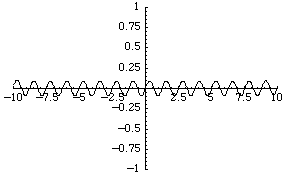
The simplest function space to compare topologies is the space of real-valued continuous functions 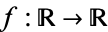 . A sequence of functions
. A sequence of functions 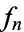 converges to
converges to 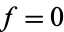 iff for every
iff for every 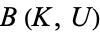 containing
containing 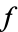 contains all but a finite number of the
contains all but a finite number of the 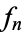 . Hence, for all
. Hence, for all 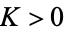 and all
and all 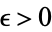 , there exists an
, there exists an 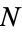 such that for all
such that for all 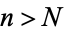 ,
,
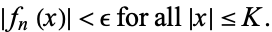 |
(2) |
For example, the sequence of functions 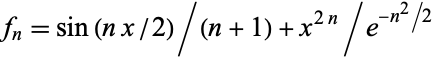 converges to the zero function, although each function is unbounded.
converges to the zero function, although each function is unbounded.
When 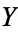 is a metric space, the compact-open topology is the same as the topology of compact convergence. If
is a metric space, the compact-open topology is the same as the topology of compact convergence. If 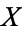 is a locally compact T2-space, a fairly weak condition, then the evaluation map
is a locally compact T2-space, a fairly weak condition, then the evaluation map
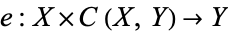 |
(3) |
defined by 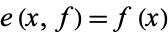 is continuous. Similarly,
is continuous. Similarly, 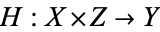 is continuous iff the map
is continuous iff the map 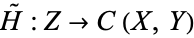 , given by
, given by 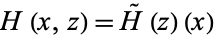 , is continuous. Hence, the compact-open topology is the right topology to use in homotopy theory.
, is continuous. Hence, the compact-open topology is the right topology to use in homotopy theory.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل شيوخ ووجهاء عشيرة البو بدري في مدينة سامراء
|
|
|