Temporal Point Process

A temporal point process is a random process whose realizations consist of the times 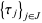 of isolated events.

Note that in some literature, the values 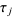 are assumed to be arbitrary real numbers while the index set  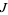is assumed to be the set  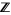of integers (Schoenberg 2002); on the other hand, some authors view temporal point processes as binary events so that  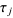takes values in a two-element set for each 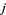, and further assume that the index set  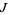is some finite set of points (Liam 2013). The prior perspective corresponds to viewing temporal point processes as how long events occur where the events themselves are spaced according to a discrete set of time parameters; the latter view corresponds to viewing temporal point processes as indications of whether or not a finite number of events has occurred.

The behavior of a simple temporal point process 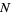 is typically modeled by specifying its conditional intensity 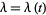. Indeed, a number of specific examples of temporal point processes are defined merely by specifying their conditional intensity functions, e.g., the Poisson and Hawkes processes.

REFERENCES:

Brillinger, D. R.; Guttorp, P. M.; and Schoenberg, F. P. "Point Processes, Temporal." Encyclopedia of Environments 3, 1577-1581, 2002.

Paninski, L. "Chapter 2: Introduction to Point Processes." 2013. https://www.stat.columbia.edu/~liam/teaching/neurostat-fall13/uri-eden-point-process-notes.pdf.

Schoenberg, F. P. "Introduction to Point Processes."