Statistical Correlation

For two random variates 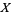 and 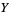, the correlation is defined bY

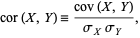(1)

where 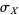 denotes standard deviation and  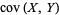is the covariance of these two variables. For the general case of variables  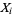and 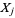, where 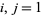, 2, ..., ,

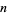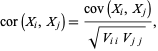(2)

where 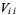 are elements of the covariance matrix. In general, a correlation gives the strength of the relationship between variables. For ,

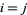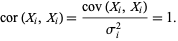(3)

The variance of any quantity is always nonnegative by definition, so

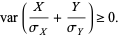(4)

From a property of variances, the sum can be expanded

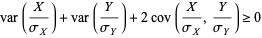(5)

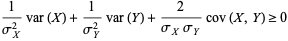(6)

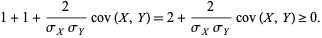(7)

Therefore,

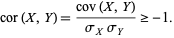(8)

Similarly,

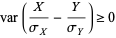(9)

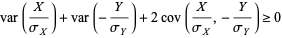(10)

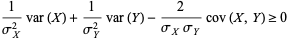(11)

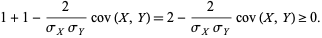(12)

Therefore,

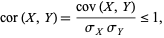(13)

so .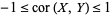

For a linear combination of two variables,

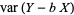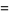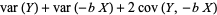			(14)
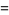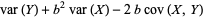			(15)
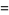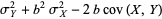			(16)
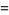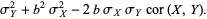			(17)

Examine the cases where ,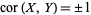

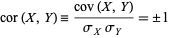(18)

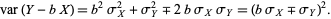(19)

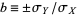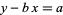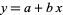The variance will be zero if , which requires that the argument of the variance is a constant. Therefore, , so . If 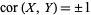,  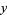is either perfectly correlated (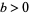) or perfectly anticorrelated (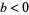) with .