
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-7-2020
Date: 20-1-2021
Date: 18-2-2020
|
Let 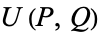 and
and 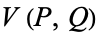 be Lucas sequences generated by
be Lucas sequences generated by 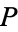 and
and 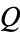 , and define
, and define
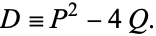 |
(1) |
Then
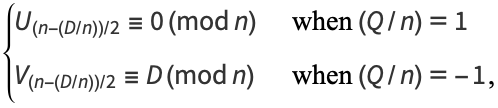 |
(2) |
where 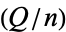 is the Legendre symbol. An odd composite number
is the Legendre symbol. An odd composite number 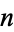 such that
such that 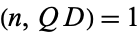 (i.e.,
(i.e., 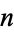 and
and 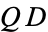 are relatively prime) is called an Euler-Lucas pseudoprime with parameters
are relatively prime) is called an Euler-Lucas pseudoprime with parameters 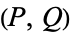 .
.
REFERENCES:
Ribenboim, P. "Euler-Lucas Pseudoprimes (elpsp(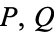 )) and Strong Lucas Pseudoprimes (slpsp(
)) and Strong Lucas Pseudoprimes (slpsp(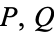 ))." §2.X.C in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 130-131, 1996.
))." §2.X.C in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 130-131, 1996.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|