المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة
الشرعية الدستورية لاقليم كردستان لإبرام العقود النفطية The contrast in adjectives Nonrestrictive modifiers in non-parenthetical positions Introduction الآفات الحشرية التي تصيب الفاصوليا السلطة الاتحادية المختصة بالتصديق في قانون ادارة الدولة العراقية للمرحلة الانتقالية السلطة الاتحادية المختصة بالتصديق في دستور العراق لسنة 2005 رأي المدقق في البيانات المالية المقارنة أو المقابلة (معيار رقم 710) تـقاريـر المـدقق عـن قـضايـا أخـرى Audit Reports On Other Issues تـقريـر مـدقق الحـسابـات فـي الولايات المتحـدة زراعة الفول والعناية به معيار 706 الفقرات التأكيدية والفقرات الأخرى في تقرير المدقق Role of Innate Immune Signals in B Cell Activation معنى قوله تعالى : فَلَمَّا نَسُوا مَا ذُكِّرُوا بِهِ فَتَحْنَا عَلَيْهِمْ أَبْوَابَ كُلِّ شَيْءٍ إجراءات المدقق في حالة عدم تمكنه من الحصول على أدلة كافية ومناسبة بسبب قيود الادارة معنى قوله تعالى : فَلَوْلَا نَفَرَ مِنْ كُلِّ فِرْقَةٍ مِنْهُمْ طَائِفَةٌ لِيَتَفَقَّهُوا فِي الدِّين

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
الشرعية الدستورية لاقليم كردستان لإبرام العقود النفطية
2025-04-15
The contrast in adjectives
2025-04-15
Nonrestrictive modifiers in non-parenthetical positions Introduction
2025-04-15
الآفات الحشرية التي تصيب الفاصوليا
2025-04-15
السلطة الاتحادية المختصة بالتصديق في قانون ادارة الدولة العراقية للمرحلة الانتقالية
2025-04-15
السلطة الاتحادية المختصة بالتصديق في دستور العراق لسنة 2005
2025-04-15

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024


Exponential Transform  
  
806   02:08 صباحاً   date: 27-10-2020
Author : Sloane, N. J. A. and Plouffe, S.
Book or Source : The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press
Page and Part : pp. 19-20


Read More
Mills, Theorem
Date: 19-3-2020 783
Surface of Revolution
Date: 22-4-2020 2736
Pythagorean Triple
Date: 9-6-2020 3409

Exponential Transform

The exponential transform is the transformation of a sequence 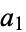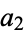a_1, a_2, ... into a sequence 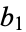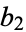b_1, b_2, ... according to the equation

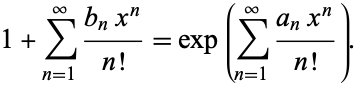1+sum_(n=1)^infty(b_nx^n)/(n!)=exp(sum_(n=1)^infty(a_nx^n)/(n!)).

The inverse ("logarithmic") transform is then given by

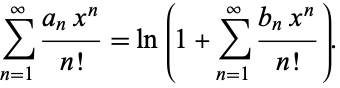sum_(n=1)^infty(a_nx^n)/(n!)=ln(1+sum_(n=1)^infty(b_nx^n)/(n!)).

The exponential transform relates the number 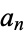a_n of labeled connected graphs on 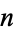n nodes satisfying some property with the corresponding total number 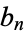b_n (not necessarily connected) of labeled graphs on 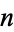n nodes. In this application, the transform is called Riddell's formula for labeled graphs.

REFERENCES:

Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, pp. 19-20, 1995.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
التاريخ / 2025-04-13

الأخبار العلمية
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
التاريخ / 2025-04-13

الساحة الاسلامية
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
التاريخ / 2025-04-15