


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات A surface of revolution is a surface generated by rotating a two-dimensional curve about an axis. The resulting surface therefore always has azimuthal symmetry. Examples of surfaces of revolution include the apple surface, cone (excluding the base), conical frustum (excluding the ends), cylinder (excluding the ends), Darwin-de Sitter spheroid, Gabriel's horn, hyperboloid, lemon surface, oblate spheroid, paraboloid, prolate spheroid, pseudosphere, sphere, spheroid, and torus (and its generalization, the toroid).
The area element of the surface of revolution obtained by rotating the curve 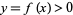 from
from 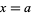 to
to 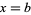 about the x-axis is
about the x-axis is
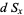 |
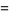 |
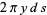 |
(1) |
 |
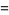 |
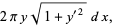 |
(2) |
so the surface area is
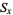 |
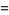 |
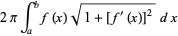 |
(3) |
 |
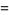 |
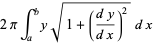 |
(4) |
(Apostol 1969, p. 286; Kaplan 1992, p. 251; Anton 1999, p. 380). If the curve is instead specified parametrically by 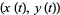 , the surface area obtained by rotating the curve about the x-axis for
, the surface area obtained by rotating the curve about the x-axis for ![t in [a,b]](https://mathworld.wolfram.com/images/equations/SurfaceofRevolution/Inline17.gif) if
if 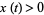 in this interval is given by
in this interval is given by
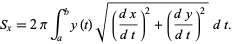 |
(5) |
Similarly, the area of the surface of revolution obtained by rotating the curve 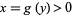 from
from 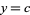 to
to 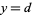 about the y-axis is given by
about the y-axis is given by
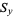 |
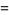 |
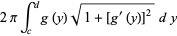 |
(6) |
 |
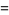 |
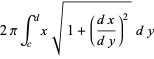 |
(7) |
(Anton 1999, p. 380). If the curve is instead specified parametrically by 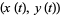 , the surface area obtained by rotating the curve about the y-axis for
, the surface area obtained by rotating the curve about the y-axis for ![t in [c,d]](https://mathworld.wolfram.com/images/equations/SurfaceofRevolution/Inline29.gif) if
if 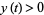 in this interval is given by
in this interval is given by
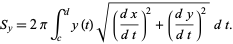 |
(8) |

The following table gives the lateral surface areas 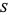 for some common surfaces of revolution where
for some common surfaces of revolution where 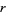 denotes the radius (of a cone, cylinder, sphere, or zone),
denotes the radius (of a cone, cylinder, sphere, or zone), 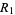 and
and 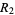 the inner and outer radii of a frustum,
the inner and outer radii of a frustum, 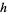 the height,
the height, 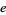 the ellipticity of a spheroid, and
the ellipticity of a spheroid, and 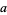 and
and 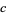 the equatorial and polar radii (for a spheroid) or the radius of a circular cross-section and rotational radius (for a torus).
the equatorial and polar radii (for a spheroid) or the radius of a circular cross-section and rotational radius (for a torus).
| surface | 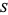 |
| cone | 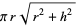 |
| conical frustum | 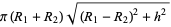 |
| cylinder | 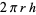 |
| oblate spheroid | 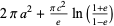 |
| prolate spheroid | 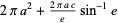 |
| sphere | 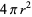 |
| torus | 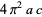 |
| zone | 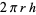 |
The standard parameterization of a surface of revolution is given by
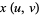 |
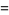 |
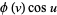 |
(9) |
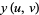 |
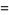 |
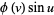 |
(10) |
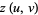 |
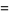 |
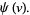 |
(11) |
For a curve so parameterized, the first fundamental form has
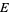 |
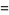 |
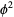 |
(12) |
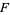 |
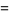 |
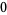 |
(13) |
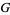 |
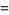 |
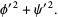 |
(14) |
Wherever 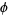 and
and 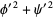 are nonzero, then the surface is regular and the second fundamental form has
are nonzero, then the surface is regular and the second fundamental form has
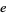 |
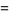 |
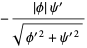 |
(15) |
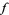 |
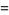 |
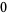 |
(16) |
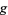 |
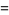 |
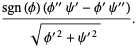 |
(17) |
Furthermore, the unit normal vector is
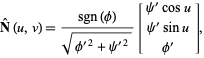 |
(18) |
and the principal curvatures are
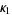 |
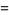 |
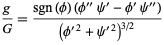 |
(19) |
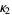 |
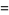 |
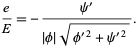 |
(20) |
The Gaussian and mean curvatures are
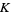 |
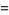 |
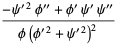 |
(21) |
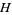 |
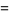 |
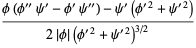 |
(22) |
(Gray 1997).
Pappus's centroid theorem gives the volume of a solid of rotation as the cross-sectional area times the distance traveled by the centroid as it is rotated.
REFERENCES:
Anton, H. Calculus: A New Horizon, 6th ed. New York: Wiley, 1999.
Apostol, T. M. Calculus, 2nd ed., Vol. 2: Multi-Variable Calculus and Linear Algebra, with Applications to Differential Equations and Probability. Waltham, MA: Blaisdell, 1969.
Gray, A. "Surfaces of Revolution." Ch. 20 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 457-480, 1997.
Hilbert, D. and Cohn-Vossen, S. "The Cylinder, the Cone, the Conic Sections, and Their Surfaces of Revolution." §2 in Geometry and the Imagination. New York: Chelsea, pp. 7-11, 1999.
Kaplan, W. Advanced Calculus, 3rd ed. Reading, MA: Addison-Wesley, 1992.
Kreyszig, E. Differential Geometry. New York: Dover, p. 131, 1991.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|