Mills' Theorem

Mills (1947) proved the existence of a real constant 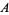 such that

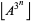(1)

is prime for all integers 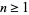, where  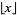is the floor function. Mills (1947) did not, however, determine 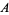, or even a range for .

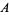A generalization of Mills' theorem to an arbitrary sequence of positive integers is given as an exercise by Ellison and Ellison (1985).

The least 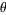 such that  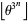is prime for all integers  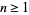is known as Mills' constant.

Mills' proof was based on the following theorem by Hoheisel (1930) and Ingham (1937). Let 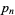 be the 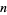th prime, then there exists a constant  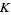such that

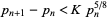(2)

for all 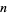. This has more recently been strengthened to

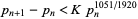(3)

(Mozzochi 1986). If the Riemann hypothesis is true, then Cramér (1937) showed that

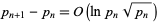(4)

(Finch 2003).

Hardy and Wright (1979) and Ribenboim (1996) point out that, despite the beauty of such prime formulas, they do not have any practical consequences. In fact, unless the exact value of 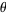 is known, the primes themselves must be known in advance to determine .

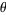REFERENCES:

Caldwell, C. "Mills' Theorem--A Generalization." http://www.utm.edu/research/primes/notes/proofs/A3n.html.

Caldwell, C. K. and Cheng, Y. "Determining Mills' Constant and a Note on Honaker's Problem." J. Integer Sequences 8, Article 05.4.1, 1-9, 2005. http://www.cs.uwaterloo.ca/journals/JIS/VOL8/Caldwell/caldwell78.html.

Ellison, W. and Ellison, F. Prime Numbers. New York: Wiley, pp. 31-32, 1985.

Finch, S. R. "Mills' Constant." §2.13 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 130-133, 2003.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Hoheisel, G. "Primzahlprobleme in der Analysis." Sitzungsber. der Preuss. Akad. Wissensch. 2, 580-588, 1930.

Ingham, A. E. "On the Difference Between Consecutive Primes." Quart. J. Math. 8, 255-266, 1937.

Mills, W. H. "A Prime-Representing Function." Bull. Amer. Math. Soc. 53, 604, 1947.

Mozzochi, C. J. "On the Difference Between Consecutive Primes." J. Number Th. 24, 181-187, 1986.

Nagell, T. Introduction to Number Theory. New York: Wiley, p. 65, 1951.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 186-187, 1996.

Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, pp. 109-110, 1991.