المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Fibonacci Prime |
 3228
 06:09 مساءً
date: 22-9-2020 |
Author : Brillhart, J.; Montgomery, P. L.; and Silverman, R. D 
Book or Source : "Tables of Fibonacci and Lucas Factorizations." Math. Comput. 50 
Page and Part : ...|
Read More
Date: 2-9-2020
771
Date: 1-11-2020
512
Date: 15-9-2020
1105
|
A Fibonacci prime is a Fibonacci number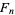 
that is also a prime number. Every 
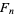that is prime must have a prime index 
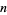, with the exception of 
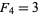. However, the converse is not true (i.e., not every prime index 
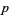gives a prime 
).
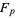The first few (possibly probable) prime Fibonacci numbers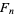 
are 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ... (OEIS A005478), corresponding to indices 
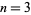, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571, 2971, 4723, 5387, ... (OEIS A001605). (Note that Gardner's statement that 
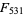is prime (Gardner 1979, p. 161) is incorrect, especially since 531 is not even prime, which it must be for 
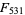to be prime.) The following table summarizes Fibonacci (possibly probable) primes with index 
.
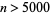| term | index | digits | discoverer | status |
| 24 | 5387 | 1126 | proven prime; https://primes.utm.edu/primes/page.php?id=51129 | |
| 25 | 9311 | 1946 | proven prime; https://primes.utm.edu/primes/page.php?id=37470 | |
| 26 | 9677 | 2023 | proven prime; https://primes.utm.edu/primes/page.php?id=35537 | |
| 27 | 14431 | 3016 | proven prime; https://primes.utm.edu/primes/page.php?id=29537 | |
| 28 | 25561 | 5342 | proven prime; https://primes.utm.edu/primes/page.php?id=24043 | |
| 29 | 30757 | 6428 | proven prime; https://primes.utm.edu/primes/page.php?id=22126 | |
| 30 | 35999 | 7523 | proven prime; https://primes.utm.edu/primes/page.php?id=20235 | |
| 31 | 37511 | 7839 | proven prime; https://primes.utm.edu/primes/page.php?id=74907 | |
| 32 | 50833 | 10624 | proven prime; https://primes.utm.edu/primes/page.php?id=75849 | |
| 33 | 81839 | 17103 | proven prime; https://primes.utm.edu/primes/page.php?id=11084 | |
| 34 | 104911 | 21925 | B. de Water, Apr. 2001 | proven prime; https://primes.utm.edu/primes/page.php?id=120463 |
| 35 | 130021 | 27173 | D. Fox, Dec. 2001 | |
| 36 | 148091 | 30949 | T. D. Noe, Feb. 12, 2003 | |
| 37 | 201107 | 42029 | H. Lifchitz, Feb. 2003 | |
| 38 | 397379 | 83047 | H. Lifchitz, Aug. 2003 | |
| 39 | 433781 | 90655 | H. Lifchitz, Sep. 2003 | |
| 40 | 590041 | 123311 | H. Lifchitz, Jan. 2005 | |
| 41 | 593689 | 124074 | H. Lifchitz, Jan. 2005 | |
| 42 | 604711 | 126377 | H. Lifchitz, Feb. 2005 | |
| 43 | 931517 | 194676 | H. Lifchitz, Sep. 2008 | |
| 44 | 1049897 | 219416 | H. Lifchitz, Oct. 2008 | |
| 45 | 1285607 | 268676 | H. Lifchitz, Nov. 2008 | |
| 46 | 1636007 | 341905 | H. Lifchitz, Mar. 2009 | |
| 47 | 1803059 | 376817 | H. Lifchitz, Jun. 2009 | |
| 48 | 1968721 | 411439 | H. Lifchitz, Nov. 2009 | |
| 49 | 2904353 | 606974 | H. Lifchitz, Jul. 2014 | |
| 50 | 3244369 | 678033 | H. Lifchitz, Sep. 2017 |
Here,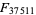 
was proven prime using the Coppersmith-Howgrave-Graham method (J. Renze, pers. comm., Aug. 16, 2005; Crandall and Pomerance 2005, p. 189), 
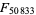was proven prime by D. Broadhurst in Oct. 2005 using a CHG proof with ECPP helpers, and 
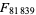(Broadhurst 2001) and 
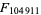(in October 2015) have also been proven to be prime.
It is not known if there are an infinite number of Fibonacci primes.
REFERENCES:
Brillhart, J.; Montgomery, P. L.; and Silverman, R. D. "Tables of Fibonacci and Lucas Factorizations." Math. Comput. 50, 251-260, 1988.
Broadhurst, D. "Fibonacci(81839) is prime." 22 Apr 2001. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0104&L=nmbrthry&P=R1807&D=0.
Caldwell, C. "Fibonacci Number." https://primes.utm.edu/top20/page.php?id=39.
Caldwell, C. "Fibonacci Prime." https://primes.utm.edu/glossary/page.php?sort=FibonacciPrime.
Crandall, R. and Pomerance, C. Prime Numbers: A Computational Perspective, 2nd ed. New York: Springer-Verlag, 2005.
Dubner, H. and Keller, W. "New Fibonacci and Lucas Primes." Math. Comput. 68, 417-427 and S1-S12, 1999.
Gardner, M. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, 1979.
Lifchitz, H. and Lifchitz, R. "PRP Top Records." https://www.primenumbers.net/prptop/searchform.php?form=F(n).
Noe, T. D. and Vos Post, J. "Primes in Fibonacci n-step and Lucas n-step Sequences." J. Integer Seq. 8, Article 05.4.4., 2005.
Pickover, C. A. Mazes for the Mind: Computers and the Unexpected. New York: St. Martin's Press, p. 350, 1993.
Pickover, C. A. A Passion for Mathematics. New York: Wiley, p. 54, 2005.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, p. 178, 1991.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
