المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Burnside Curve |
 865
 01:57 صباحاً
date: 6-7-2020 |
Author : Brezhnev, Y. V. 
Book or Source : "Uniformisation: On the Burnside Curve y^2=x^5-x." 9 Dec 2001. https://arxiv.org/abs/math.CA/0111150. 
Page and Part : ...|
Read More
Date: 13-8-2020
949
Date: 28-12-2020
843
Date: 20-2-2020
880
|
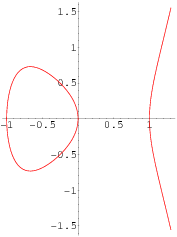
The only known classically known algebraic curve of curve genus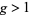 
that has an explicit parametrization 
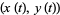in terms of standard special functions (Burnside 1893, Brezhnev 2001). This equation is given by
 |
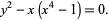(1) |
The closed portion of the curve has area
 |
 |
 |
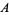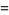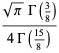(2) |
 |
 |
 |
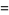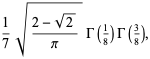(3) |
where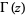 
is a gamma function.
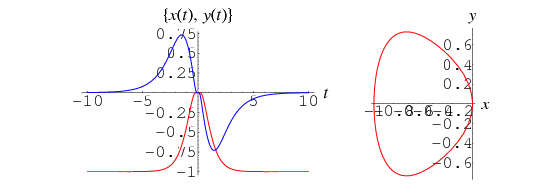
The closed portion of this curve has a parametrization in terms of the Weierstrass elliptic function given by
 |
 |
 |
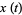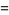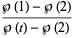(4) |
 |
 |
 |
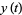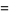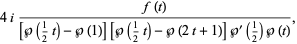(5) |
where
![f(t)=[P(t)-P(2t)][P(1/2t)-P(t)][P(1/2t)-P(t+2)]×[P(1/2)-P(2t+1)][P(1/2)-P(1)],](https://mathworld.wolfram.com/images/equations/BurnsideCurve/NumberedEquation2.gif) |
(6) |
the half-periods are given by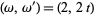 
and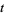 
ranges over complex values (Brezhnev 2001).
REFERENCES:
Brezhnev, Y. V. "Uniformisation: On the Burnside Curve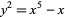 
." 9 Dec 2001. https://arxiv.org/abs/math.CA/0111150.
Burnside, W. S. "Note on the Equation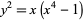 
." Proc. London Math. Soc. 24, 17-20, 1893.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|
