Voronin Universality Theorem

Voronin (1975) proved the remarkable analytical property of the Riemann zeta function 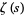 that, roughly speaking, any nonvanishing analytic function can be approximated uniformly by certain purely imaginary shifts of the zeta function in the critical strip.

More precisely, let 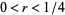 and suppose that  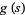is a nonvanishing continuous function on the disk  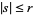that is analytic in the interior. Then for any 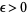, there exists a positive real number  such that

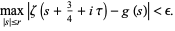Moreover, the set of these  has positive lower density, i.e.,

Garunkštis (2003) obtained explicit estimates for the first approximating  and the positive lower density, provided that 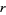 is sufficiently small and  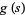sufficiently smooth. The condition that  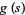have no zeros for  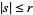is necessary.

The Riemann hypothesis is known to be true iff 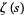 can approximate itself uniformly in the sense of Voronin's theorem (Bohr 1922, Bagchi 1987). It is also known that there exists a rich zoo of Dirichlet series having this or some similar universality property (Karatsuba 1992, Laurinčikas 1996, Matsumoto 2001).

REFERENCES:

Bagchi, B. "Recurrence in Topological Dynamics and the Riemann Hypothesis." Acta Math. Hungar. 50, 227-240, 1987.

Bohr, H. "Über eine Quasi-Periodische Eigenschaft Dirichletscher Reihen mit Anwendung auf die Dirichletschen 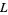-Funktionen." Math. Ann. 85, 115-122, 1922.

Garunkštis, R. "The Effective Universality Theorem for the Riemann Zeta Function." Bonner math. Schriften 360, 2003.

Karatsuba, A. A. and Voronin, S. M. The Riemann Zeta-Function. Hawthorn, NY: de Gruyter, 1992.

Laurinčikas, A. Limit Theorems for the Riemann Zeta-Function. Dordrecht, Netherlands: Kluwer, 1996.

Matsumoto, K. "Probabilistic Value-Distribution Theory of Zeta Functions." Sugaku 53, 279-296, 2001. Reprinted in Sugaku Expositions 17, 51-71, 2004.

Voronin, S. M. "Theorem on the Universality of the Riemann Zeta Function." Izv. Akad. Nauk SSSR, Ser. Matem. 39, 475-486, 1975. Reprinted in Math. USSR Izv. 9, 443-445, 1975.