Schur's Partition Theorem

Schur's partition theorem lets 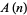 denote the number of partitions of  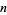into parts congruent to  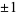(mod 6),  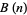denote the number of partitions of  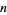into distinct parts congruent to  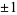(mod 3), and  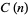the number of partitions of  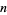into parts that differ by at least 3, with the added constraint that the difference between multiples of three is at least 6. Then  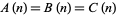(Schur 1926; Bressoud 1980; Andrews 1986, p. 53).

The values of 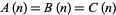 for 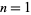, 2, ... are 1, 1, 1, 1, 2, 2, 3, 3, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, ... (OEIS A003105). For example, for 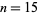, there are nine partitions satisfying these conditions, as summarized in the following table (Andrews 1986, p. 54).

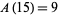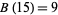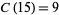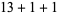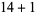		15

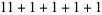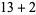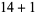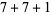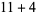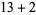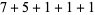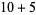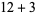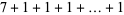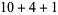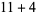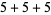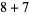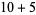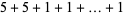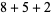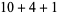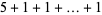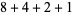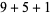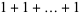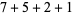The identity 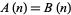 can be established using the identity

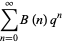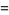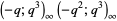			(1)
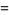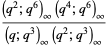			(2)
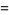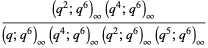			(3)
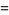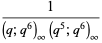			(4)
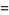			(5)

(Andrews 1986, p. 54). The identity 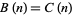 is significantly trickier.

REFERENCES:

Andrews, G. E. "q-Series and Schur's Theorem" and "Bressoud's Proof of Schur's Theorem." §6.2-6.3 in q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 53-58, 1986.

Bressoud, D. M. "Combinatorial Proof of Schur's 1926 Partition Theorem." Proc. Amer. Math. Soc. 79, 338-340, 1980.

Schur, I. "Über die Kongruenz 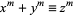 (mod 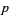)." Jahresber. Deutsche Math.-Verein. 25, 114-116, 1916.

Schur, I. "Zur additiven Zahlentheorie." Sitzungsber. Preuss. Akad. Wiss. Phys.-Math. Kl., pp. 488-495, 1926. Reprinted in Gesammelte Abhandlungen, Vol. 3. Berlin: Springer-Verlag, pp. 43-50, 1973.

Sloane, N. J. A. Sequence A003105/M0254 in "The On-Line Encyclopedia of Integer Sequences."