Schlömilch's Series

A Fourier series-like expansion of a twice continuously differentiable function

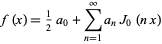(1)

for 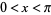, where  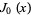is a zeroth order Bessel function of the first kind. The coefficients are then given by

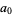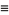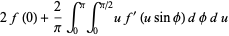			(2)
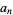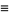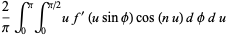			(3)

(Gradshteyn and Ryzhik 2000, p. 926), where 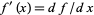 and care should be taken to avoid the two typos of Iyanaga and Kawada (1980) and Itô (1986).

As an example, consider 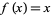, which has  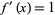and therefore

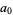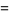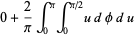			(4)
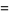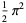			(5)
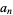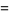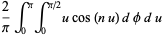			(6)
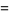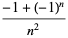			(7)
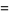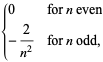			(8)

so

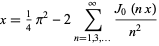(9)

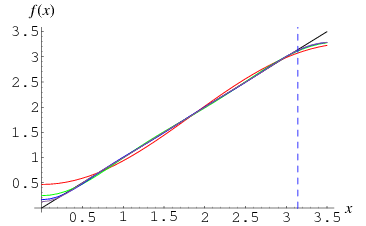
(Whittaker and Watson 1990, p. 378; Gradshteyn and Ryzhik 2000, p. 926). This is illustrated above with 1 (red), 2 (green), 3 (blue), and 4 terms (violet) included.

Similarly, for ,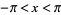

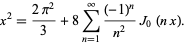(10)

REFERENCES:

Gradshteyn, I. S. and Ryzhik, I. M. "The Series 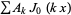." Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 926, 2000.

Itô, K. (Ed.). Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 2. Cambridge, MA: MIT Press, p. 1803, 1986.

Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1473, 1980.

Schlömilch. Z. für Math. Phys. 3, 137-165, 1857.

Whittaker, E. T. and Watson, G. N. "Schlömilch's Expansion of an Arbitrary Function in a Series of Bessel Coefficients of Order Zero." §17.82 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 377-378, 1990.