


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-11-2018
Date: 18-11-2018
Date: 18-10-2018
|
 |
 |
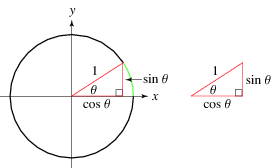
The sine function 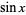 is one of the basic functions encountered in trigonometry (the others being the cosecant, cosine, cotangent, secant, and tangent). Let
is one of the basic functions encountered in trigonometry (the others being the cosecant, cosine, cotangent, secant, and tangent). Let 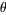 be an angle measured counterclockwise from the x-axis along an arc of the unit circle. Then
be an angle measured counterclockwise from the x-axis along an arc of the unit circle. Then 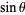 is the vertical coordinate of the arc endpoint, as illustrated in the left figure above.
is the vertical coordinate of the arc endpoint, as illustrated in the left figure above.
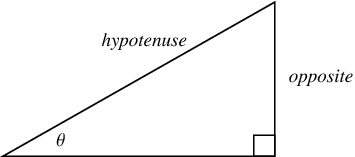
The common schoolbook definition of the sine of an angle 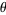 in a right triangle (which is equivalent to the definition just given) is as the ratio of the lengths of the side of the triangle opposite the angle and the hypotenuse, i.e.,
in a right triangle (which is equivalent to the definition just given) is as the ratio of the lengths of the side of the triangle opposite the angle and the hypotenuse, i.e.,
 |
(1) |
A convenient mnemonic for remembering the definition of the sine, as well as the cosine and tangent, is SOHCAHTOA (sine equals opposite over hypotenuse, cosine equals adjacent over hypotenuse, tangent equals opposite over adjacent).
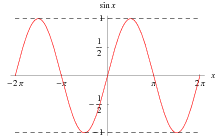
As a result of its definition, the sine function is periodic with period 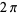 . By the Pythagorean theorem,
. By the Pythagorean theorem, 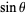 also obeys the identity
also obeys the identity
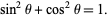 |
(2) |
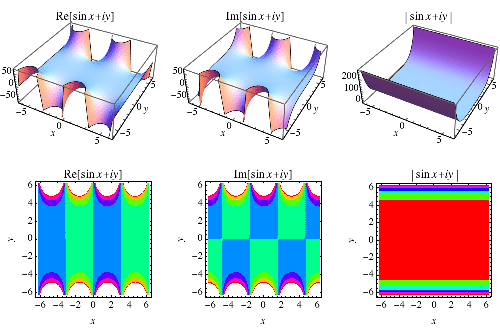 |
The definition of the sine function can be extended to complex arguments 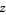 , illustrated above, using the definition
, illustrated above, using the definition
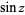 |
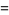 |
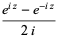 |
(3) |
 |
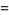 |
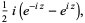 |
(4) |
where e is the base of the natural logarithm and i is the imaginary number. Sine is an entire function and is implemented in the Wolfram Language as Sin[z].
A related function known as the hyperbolic sine is similarly defined,
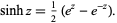 |
(5) |
The sine function can be defined analytically by the infinite sum
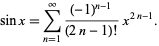 |
(6) |
It is also given by the imaginary part of the complex exponential
![sinx=I[e^(ix)].](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation5.gif) |
(7) |
The multiplicative inverse of the sine function is the cosecant, defined as
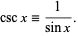 |
(8) |
The sine function is also given by the limit
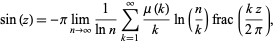 |
(9) |
where 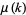 is the Möbius function and
is the Möbius function and 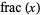 is the fractional part (M. Trott).
is the fractional part (M. Trott).
The derivative of 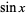 is
is
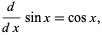 |
(10) |
and its indefinite integral is
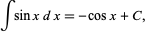 |
(11) |
where 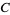 is a constant of integration.
is a constant of integration.
Using the results from the exponential sum formulas
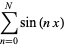 |
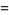 |
![I[sum_(n=0)^(N)e^(inx)]](http://mathworld.wolfram.com/images/equations/Sine/Inline20.gif) |
(12) |
 |
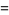 |
![I[(e^(i(N+1)x)-1)/(e^(ix)-1)]](http://mathworld.wolfram.com/images/equations/Sine/Inline23.gif) |
(13) |
 |
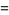 |
![I[(e^(i(N+1)x/2))/(e^(ix/2))(e^(i(N+1)x/2)-e^(-i(N+1)x/2))/(e^(ix/2)-e^(-ix/2))]](http://mathworld.wolfram.com/images/equations/Sine/Inline26.gif) |
(14) |
 |
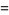 |
![(sin(1/2(N+1)x))/(sin(1/2x))I[e^(iNx/2)]](http://mathworld.wolfram.com/images/equations/Sine/Inline29.gif) |
(15) |
 |
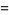 |
![(sin(1/2Nx)sin[1/2(N+1)x])/(sin(1/2x)).](http://mathworld.wolfram.com/images/equations/Sine/Inline32.gif) |
(16) |
Similarly,
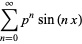 |
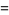 |
![I[sum_(n=0)^(infty)p^ne^(inx)]](http://mathworld.wolfram.com/images/equations/Sine/Inline35.gif) |
(17) |
 |
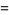 |
![I[(1-pe^(-ix))/(1-2pcosx+p^2)]](http://mathworld.wolfram.com/images/equations/Sine/Inline38.gif) |
(18) |
 |
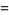 |
 |
(19) |
The sum of 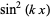 can also be done in closed form,
can also be done in closed form,
![sum_(k=0)^Nsin^2(kx)=1/4{1+2N-cscxsin[x(1+2N)]}.](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation10.gif) |
(20) |
A related sum identity is given by
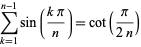 |
(21) |
(T. Drane, pers. comm., Apr. 19, 2006).
Product identities include
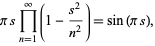 |
(22) |
which is more commonly written as an identity for the sinc function or in the form
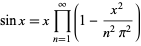 |
(23) |
(Edwards 2001, pp. 18 and 47; Borwein et al. 2004, p. 5). Another product formula is
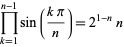 |
(24) |
(T. Drane, pers. comm., Apr. 19, 2006).
The sine function obeys the identity
![sin(ntheta)=2costhetasin[(n-1)theta]-sin[(n-2)theta]](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation15.gif) |
(25) |
and the multiple-angle formula
![sin(nx)=sum_(k=0)^n(n; k)cos^kxsin^(n-k)xsin[1/2(n-k)pi],](http://mathworld.wolfram.com/images/equations/Sine/NumberedEquation16.gif) |
(26) |
where 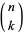 is a binomial coefficient. It is related to
is a binomial coefficient. It is related to 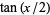 via
via
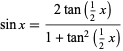 |
(27) |
(Trott 2006, p. 39).
A curious identity is given by
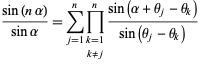 |
(28) |
for all 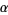 and
and 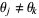 (Calogero 1999; Beylkin and Mohlenkamp 2002; Trott 2005, pp. 5-6).
(Calogero 1999; Beylkin and Mohlenkamp 2002; Trott 2005, pp. 5-6).
Cvijović and Klinowski (1995) show that the sum
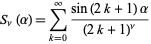 |
(29) |
has closed form for 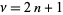 ,
,
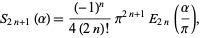 |
(30) |
where 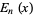 is an Euler polynomial.
is an Euler polynomial.
A continued fraction representation of 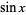 is
is
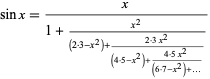 |
(31) |
(Olds 1963, p. 138).
The value of 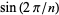 is irrational for all integers
is irrational for all integers 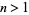 except 2, 4, and 12, for which
except 2, 4, and 12, for which 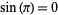 ,
, 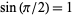 , and
, and 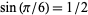 , respectively, a result that is essentially known as Niven's theorem.
, respectively, a result that is essentially known as Niven's theorem.
The Fourier transform of 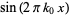 is given by
is given by
](http://mathworld.wolfram.com/images/equations/Sine/Inline56.gif) |
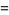 |
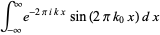 |
(32) |
 |
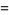 |
![1/2i[delta(k+k_0)-delta(k-k_0)].](http://mathworld.wolfram.com/images/equations/Sine/Inline61.gif) |
(33) |
A definite integral involving 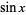 is given by
is given by
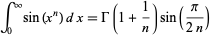 |
(34) |
for 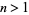 where
where 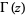 is the gamma function (R. Mabry, pers. comm., Dec. 15, 2005; T. Drane, pers. comm., Apr. 21, 2006).
is the gamma function (R. Mabry, pers. comm., Dec. 15, 2005; T. Drane, pers. comm., Apr. 21, 2006).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Circular Functions." §4.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 71-79, 1972.
Beylkin, G. and Mohlenkamp, M. J. Proc. Nat. Acad. Sci. USA 99, 10246, 2002.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 225, 1987.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Calogero, F. "Remarkable Matrices and Trigonometric Identities. II." Commun. Appl. Math. 3, 267-270, 1999.
Cvijović, D. and Klinowski, J. "Closed-Form Summation of Some Trigonometric Series." Math. Comput. 64, 205-210, 1995.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Project Mathematics. "Sines and Cosines, Parts I-III." Videotape. http://www.projectmathematics.com/sincos1.htm.
Jeffrey, A. "Trigonometric Identities." §2.4 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 111-117, 2000.
Spanier, J. and Oldham, K. B. "The Sine 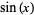 and Cosine
and Cosine 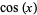 Functions." Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Functions." Ch. 32 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 295-310, 1987.
Tropfke, J. Teil IB, §1. "Die Begriffe des Sinus und Kosinus eines Winkels." In Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter, fünfter Band, zweite aufl. Berlin and Leipzig, Germany: de Gruyter, pp. 11-23, 1923.
Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.
Zwillinger, D. (Ed.). "Trigonometric or Circular Functions." §6.1 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 452-460, 1995.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
أولياء أمور الطلبة يشيدون بمبادرة العتبة العباسية بتكريم الأوائل في المراحل المنتهية
|
|
|