
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-11-2018
Date: 18-10-2018
Date: 24-10-2018
|
The logarithmic capacity of a compact set 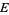 in the complex plane is given by
in the complex plane is given by
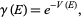 |
(1) |
where
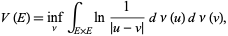 |
(2) |
and  runs over each probability measure on
runs over each probability measure on 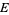 . The quantity
. The quantity 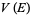 is called the Robin's constant of
is called the Robin's constant of 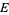 and the set
and the set 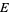 is said to be polar if
is said to be polar if 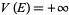 or equivalently,
or equivalently, 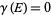 .
.
The logarithmic capacity coincides with the transfinite diameter of 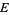 ,
,
![lim_(n->infty)max_({w_1,...,w_n} subset E)(product_(1<=j<k<=n)|w_j-w_k|)^(2/[n(n-1)]).](http://mathworld.wolfram.com/images/equations/LogarithmicCapacity/NumberedEquation3.gif) |
(3) |
If 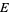 is simply connected, the logarithmic capacity of
is simply connected, the logarithmic capacity of 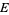 is equal to the conformal radius of
is equal to the conformal radius of 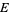 . Tables of logarithmic capacities have been calculated (e.g., Rumely 1989).
. Tables of logarithmic capacities have been calculated (e.g., Rumely 1989).
REFERENCES:
Hille, E. Analytic Function Theory. New York: Chelsea, 1973.
Rumely, R. Capacity Theory on Algebraic Curves. New York: Springer-Verlag, pp. 348-351, 1989.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|