المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Krichever-Novikov Equation |
 2946
 03:01 مساءً
date: 21-7-2018 |
Author : Krichever, I. M. and Novikov, S. P 
Book or Source : "Holomorphic Bundles over Algebraic Curves, and Nonlinear Equations." Russ. Math. Surv. 35, 53-80, 1980. English translation of Uspekhi Mat. Nauk 35 
Page and Part : ...|
Read More
Date: 25-7-2018
2039
Date: 21-7-2018
2216
Date: 25-7-2018
1490
|
The partial differential equation
 |
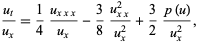where
 |
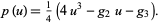The special cases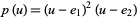 
and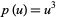 
can be reduced to the Korteweg-de Vries equation by a change of variables.
REFERENCES:
Krichever, I. M. and Novikov, S. P. "Holomorphic Bundles over Algebraic Curves, and Nonlinear Equations." Russ. Math. Surv. 35, 53-80, 1980. English translation of Uspekhi Mat. Nauk 35, 47-68, 1980.
Mokhov, O. I. "Canonical Hamiltonian Representation of the Krichever-Novikov Equation." Math. Notes 50, 939-945, 1991. English translation of Mat. Zametki 50, 87-96, 1991.
Novikov, D. P. "Algebraic-Geometric Solutions of the Krichever-Novikov Equation." Theoret. Math. Phys. 121, 1567-15773, 1999.
Sokolov, V. V. "Hamiltonian Property of the Krichever-Novikov Equation." Dokl. Akad. Nauk SSSR 277, 48-50, 1984.
Svinolupov, S. I.; Sokolov, V. V.; and Yamilov, R. I. "Bäcklund Transformations for Integrable Evolution Equations." Dokl. Akad. Nauk SSSR 271, 802-805, 1983. English translation of Sov. Math. Dokl. 28, 165-168, 1983.
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل شيوخ ووجهاء عشيرة البو بدري في مدينة سامراء
|
|
|
