Poisson's equation

We have seen that the electric field generated by a set of stationary charges can be written as the gradient of a scalar potential, so that

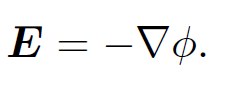 (1.1)

This equation can be combined with the field

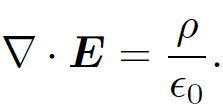
To give a partial differential equation for the scalar potential:

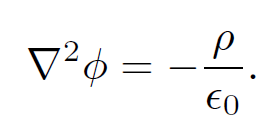 (1.2)

This is an example of a very famous type of partial differential equation known as ''Poisson's equation." In its most general form Poisson's equation is written

 (1.3)

where u(r) is some scalar potential which is to be determined and v(r) is a known ''source function." The most common boundary condition applied to this equation is that the potential u is zero at infinity. The solutions to Poisson's equation are completely superposable. Thus, if u₁ is the potential generated by the source function v₁, and u₂ is the potential generated by the source function v₂, so that

 (1.4)

then the potential generated by v₁ + v₂ is u₁ + u₂, since

 (1.5)

Poisson's equation has this property because it is linear in both the potential and the source term. The fact that the solutions to Poisson's equation are superposable suggests a general method for solving this equation. Suppose that we could construct all of the solutions generated by point sources. Of course, these solutions must satisfy the appropriate boundary conditions. Any general source function can be built up out of a set of suitably weighted point sources, so the general solution of Poisson's equation must be expressible as a weighted sum over the point source solutions. Thus, once we know all of the point source solutions we can construct any other solution. In mathematical terminology we require the solution to

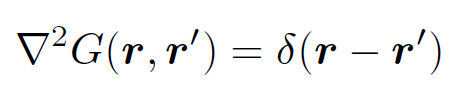 (1.6)

which goes to zero as |r| → ∞. The function G(r, rʹ) is the solution generated by a point source located at position rʹ. In mathematical terminology this function is known as a ''Green's function". The solution generated by a general source function v(r) is simply the appropriately weighted sum of all of the Green's function solutions:

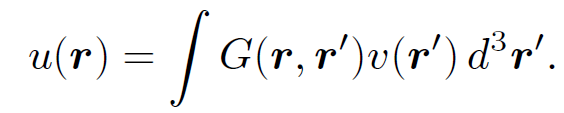 (1.7)

We can easily demonstrate that this is the correct solution:

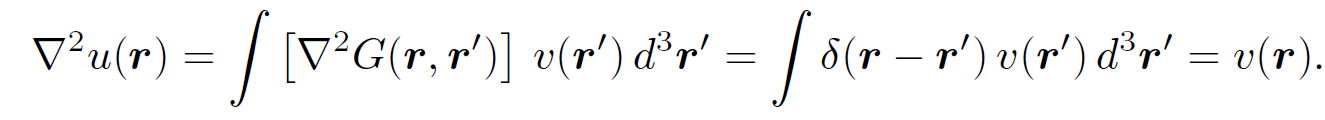 (1.8)

Let us return to Eq. (1.2):

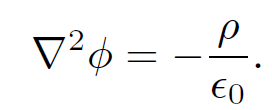 (1.9)

The Green's function for this equation satisfies Eq. (1.6) with |G| → ∞ as |r| → 0. That

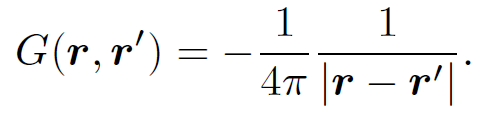 (1.10)

That the Green's function has the same form as the potential generated by a point charge. This is hardly surprising given the definition of a Green's function. It follows from Eq. (1.7) and (1.10) that the general solution to Poisson's equation (1.9) is written

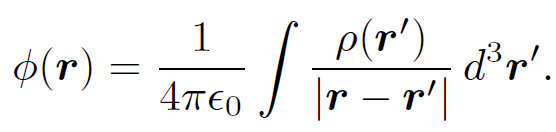 (1.11)

In fact, we have already obtained this solution by another method.