Electronic spectra of octahedral and tetrahedral complexes

   Electronic spectroscopy is a complicated topic and we shall restrict our discussion to high-spin complexes. The spectrum of [Ti)H₂O(₆]³⁺‏ (Figure 20.4) exhibits one broad band; close inspection shows the presence of a shoulder indicating that the absorption is actually two closely spaced bands arising from a Jahn–Teller effect in the excited state. The term symbol for the ground state of Ti³⁺‏ (d¹, one electron for which m_l = 2, L = 2, S = 1/2 ) is ²D. In an octahedral field, this is split into ²T_2g and ²E_g terms separated by energy Δ_oct, the magnitude of which increases with increasing field strength (Figure 1.1).

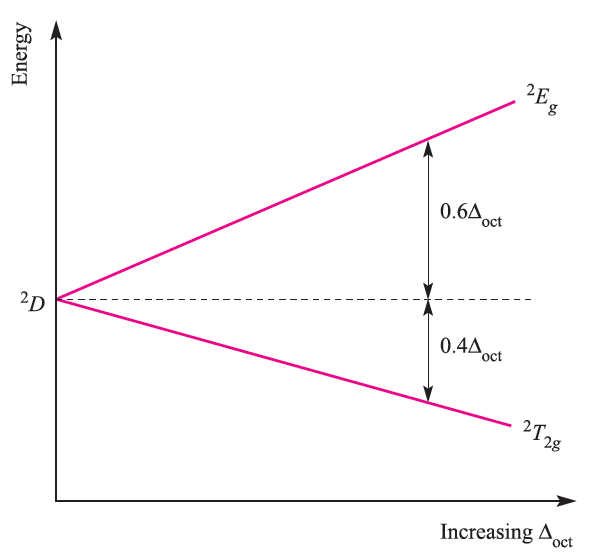
Fig. 1.1 Energy level diagram for a d¹ ion in an octahedral field.

   The electronic spectrum of Ti³⁺‏ arises from a transition from the T_2g to E_g term; the energy of the transition depends on the field strength of the ligands in the octahedral Ti(III) complex. For the d⁹ configuration (e.g. Cu²⁺‏) in an octahedral field (actually, a rare occurrence because of Jahn–Teller effects which lower the symmetry), the ground state of the free ion (²D) is again split into ²T_2g and ²E_g terms, but, in contrast to the d1 ion (Figure 1.1), the ²E_g term is lower than the ²T_2g term. The d⁹ and d¹ configurations are related by a positive hole concept: d⁹ is derived from a d¹⁰ configuration by replacing one electron by a positive hole; thus, whereas the d¹ configuration contains one electron, d⁹ contains one ‘hole’ (see Box 20.6). For a d⁹ ion in an octahedral field, the splitting diagram is an inversion of that for the octahedral d¹ ion. This relationship is shown in Figure 1.2 (an Orgel diagram) where the right-hand side describes the octahedral d1 case and the left-hand side, the octahedral d⁹ ion. Just as there is a relationship between the d¹ and d⁹ configurations, there is a similar relationship between the d⁴ and d⁶ configurations. Further, we can relate the four configurations in an octahedral field as follows. In the weak-field limit, a d⁵ ion is high-spin and spherically symmetric, and in this latter regard, d⁰, d⁵ and d¹⁰ configurations are analogous. Addition of one electron to the high-spin d⁵ ion to give a d⁶ configuration mimics going from a d⁰ to d¹ configuration; likewise, going from d⁵ to d⁴ by adding a positive hole mimics going from d¹⁰ to d⁹. The result is that the Orgel diagrams for octahedral d1 and d⁶ ions are the same, as are the diagrams for octahedral d⁴ and d⁹ (Figure 1.2).

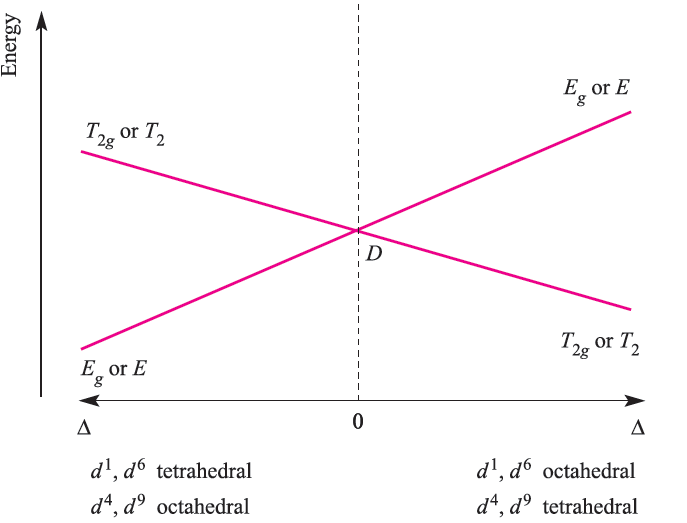
Fig. 1.2 Orgel diagram for d¹, d⁴ (high-spin), d⁶  (highspin) and d⁹ ions in octahedral (for which T_2g and E_g labels are relevant) and tetrahedral (E and T₂ labels) fields. In contrast to Figure 1.1, multiplicities are not stated  because they depend on the dⁿ configuration.

   Figure 1.2 also shows that the diagram for a d¹ or d⁹ ion is inverted by going from an octahedral to tetrahedral field.  Because the Orgel diagram uses a single representation for octahedral and tetrahedral fields, it is not possible to indicate that Δ_tet = 4/9Δ_oct. Tetrahedral d⁴ and d⁶ ions can also be represented on the same   Orgel diagram.   Finally, Figure 1.2 shows that for each of the octahedral and tetrahedral d¹, d⁴, d⁶ and d⁹ ions, only one electronic transition  from a ground to excited state is possible:

• for octahedral d¹ and d⁶, the transition is E_g←T_2g
• for octahedral d⁴ and d⁹, the transition is T_2g←E_g
• for tetrahedral d¹ and d⁶, the transition is T₂←E
• for tetrahedral d⁴ and d⁹, the transition is E←T₂

   Each transition is spin-allowed (no change in total spin, S) and the electronic spectrum of each ion exhibits one absorption. For sake of completeness, the notation for the transitions given above should include spin multiplicities, 2S ‏+ 1  , e.g. for octahedral d¹, the notation is ²E_g←²T_2g, and for high-spin, octahedral d⁴, ⁵T_2g←⁵E_g.  In an analogous manner to grouping d¹, d⁴, d⁶ and d⁹ ions, we can consider together d 2, d³, d⁷ and d⁸ ions in octahedral and tetrahedral fields. Two terms arise for the d² ion: ³F (ground state) and ³P (excited state); deriving terms from a table of microstates is dealt with in the next subsection. In an octahedral field, the ³P term does not split, and is labelled ³T_1g. The 3F term splits into ³T_1g, ³T_2g and ³A_2g terms. The ³T_1g(F) term corresponds to a t_2g 2e_g⁰ arrangement and is triply degenerate because there are three ways of placing two electrons (with parallel spins) in any two of the d_xy, d_yz and d_xz orbitals. The ³A_2g term corresponds to t_2g⁰ e_g² arrangement (singly degenerate).

  The ³T_2g and ³T_1g)P( terms equate with a t_2g¹ e_g¹ configuration; the lower energy ³T_2g term arises from placing two electrons in orbitals lying in mutually perpendicular planes, e.g. (d_xy)¹(d_z²)¹, while the higher energy ³T_1g(P) term arises from placing two electrons in orbitals lying in the same plane e.g. (d_xy)¹(d_x²_-y²)¹. The energies of the ³T_1g(F), ³T_2g, ³A_2g and ³T_1g(P( terms are shown on the right-hand side of Figure 1.3; note the effect of increasing field strength. Starting from this diagram and using the same arguments as for the d¹, d⁴, d⁶ and d⁹ ions, we can derive the complete Orgel diagram shown in Figure 1.3. At increased field strengths, the lines describing the T_1g(F) and T_1g(P (terms (or T₁, depending on whether we are dealing with octahedral or tetrahedral cases) curve away from one another; there is interaction between terms of the same symmetry and they are not allowed to cross (the non-crossing rule). From Figure 1.3, we can see why three absorptions are observed in the electronic spectra of d², d³, d⁷ and d⁸ octahedral and tetrahedral complexes; the transitions are from the ground to excited states, and are all spin-allowed. Transitions are possible from one excited state to another, but their probability is so low that they can be ignored. Figure 20.19 illustrates spectra for octahedral nickel(II) (d⁸) complexes.

  For the high-spin d⁵ configuration, all transitions are spinforbidden and ‘d–d’ transitions that are observed are between the 6S ground state and quartet states (three unpaired electrons).

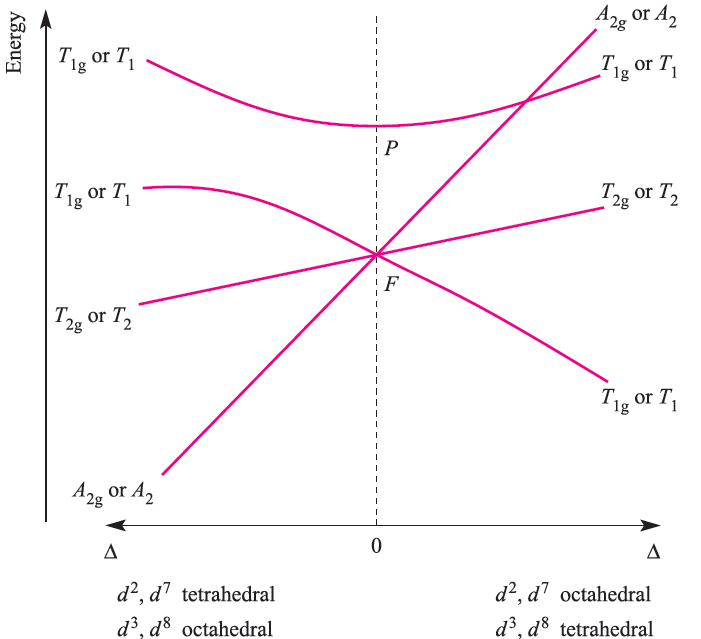
Fig. 1.3 Orgel diagram for d², d³, d⁷ and d⁸ ions (highspin) in octahedral (for which T_1g, T_2g and A_2g labels arerelevant) and tetrahedral (T₁, T₂ and A₂ labels) fields. Multiplicities are not stated because they depend on the d n configuration, e.g. for the octahedral d² ion, ₃T_1g, ³T_2g and ³A_2g labels are appropriate.

   Associated absorptions are extremely weak.  For a proper interpretation of electronic spectral features, interelectronic interaction must be taken into account and parameters additional to Δ_oct are needed to quantify the description of the spectrum. There are Racah parameters which we shall meet again when we describe Tanabe–Sugano diagrams. The evaluation of Δ_oct from electronic spectra is, therefore, more difficult for d² (and related dⁿ) than for d¹ (and d⁶ etc.) ions and some uncertainty is often associated with reported values.