


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 28-7-2016
Date: 26-8-2016
Date: 11-8-2016
|
Diatomic Molecules in Two Dimensions
You have been transported to a two-dimensional world by an evil wizard who refuses to let you return to your beloved Columbia unless you can determine the thermodynamic properties for a rotating heteronuclear diatomic molecule constrained to move only in a plane (two dimensions). You may assume in what follows that the diatomic molecule does not undergo translational motion. Indeed, it only has rotational kinetic energy about its center of mass. The quantized energy levels of a diatomic in two dimensions are

with degeneracies gJ = 2, for J not equal to zero, and gJ = 1 when J = 0. As usual, B = h/8π2 Ic, where I is the moment of inertia.
Hint: For getting out of the wizard’s evil clutches, treat all levels as having the same degeneracy and then... . Oh, no! He’s got me, too!
a) Assuming τ >> hcB, derive the partition function Zrot for an individual diatomic molecule in two dimensions.
b) Determine the thermodynamic energy E and heat capacity CV in the limit, where τ >> hcB for a set of indistinguishable, independent, heteronuclear diatomic molecules constrained to rotate in a plane. Compare these results to those for an ordinary diatomic rotor in three dimensions. Comment on the differences and discuss briefly in terms of the number of degrees of freedom required to describe the motion of a diatomic rotor confined to a plane.
SOLUTION
a) The partition function Zrot may be calculated in the usual way by multiplying the individual Boltzmann factors by their degeneracies and summing:
 (1)
(1)
This is difficult to sum, but we may consider the integral instead, given the assumption that τ >> hcB:
 (2)
(2)
b) The energy and heat capacity of the set of diatomic molecules described above may be determined from the partition function for the set:
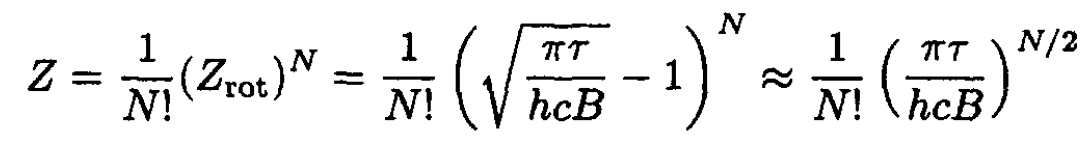 (3)
(3)
where the N-fold product has been divided by the number of permutations of the N indistinguishable molecules. Recall that

We then find that
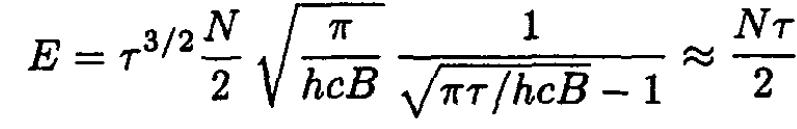 (4)
(4)
Again, for τ >> hcB, the heat capacity is
 (5)
(5)
A diatomic rotor in three dimensions would have contributions to the energy of (1/2)τ per degree of freedom. Three degrees of translation and two degrees of rotation (assuming negligible inertia perpendicular to its length) gives for one molecule
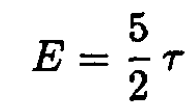 (6)
(6)
 (7)
(7)
A diatomic rotor confined to a plane would have three degrees of freedom, two translational and one rotational. Hence,
 (8)
(8)
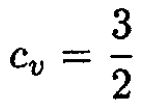 (9)
(9)
The quantization of energy is not apparent since we have assumed τ >> hcB.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|