


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 7-8-2016
Date: 14-8-2016
Date: 1-8-2016
|
Three Spins
Consider three particles of spin 1/2 which have no motion. The raising (s+ = sx + isy) and lowering (s- = sx - isy) operators of the individual spins have the property
 (i)
(i)
 (ii)
(ii)
where the arrows indicate the spin orientation with regard to the z-direction.
a) Write explicit wave functions for the four J = 3/2 states: (M = 3/2, 1/2, -1/2, -3/2).
b) Using the definition that 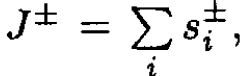 construct the 4 × 4 matrices which represent the J+ and J- operators.
construct the 4 × 4 matrices which represent the J+ and J- operators.
c) Construct the 4 × 4 matrices which represent Jx and Jy.
d) Construct from Jx, Jy, Jz the value of the matrix J2.
SOLUTION
a) We use the notation that the state with three spins up is |↑1↑2↑3⟩. This is the state with M = 3/2. We operate on this with the lowering operator J-, which shows that the states |3/2, M⟩ with lower values of M are
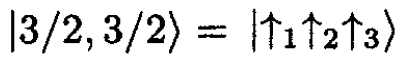 (1)
(1)
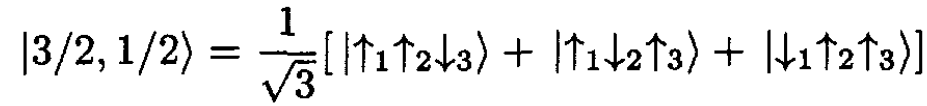 (2)
(2)
 (3)
(3)
 (4)
(4)
b) From the definition of J+ we deduce that
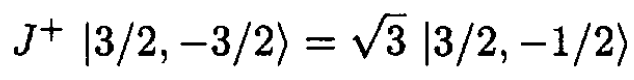 (5)
(5)
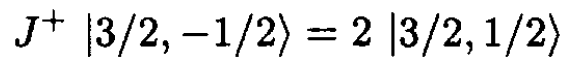 (6)
(6)
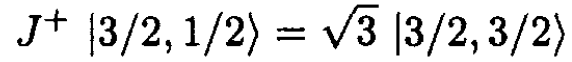 (7)
(7)
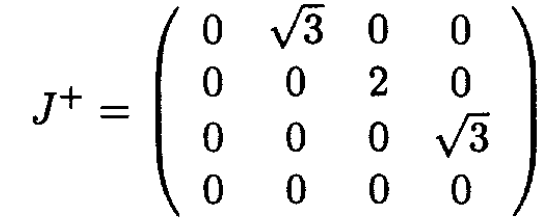 (8)
(8)
The matrix J- is the Hermitian conjugate of J+:
 (9)
(9)
c) Because Jx = (J+ + J-)/2 and Jy = -i (J+ - J-)/2 we can construct
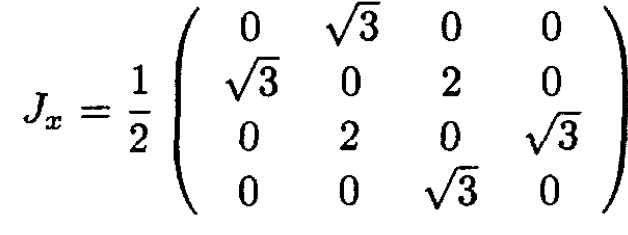 (10)
(10)
 (11)
(11)
 (12)
(12)
d) To find the matrix J2 = J2x + J2y + J2z, we square each of the three matrices and add them. This gives J2 = 15Ĩ/4, where Ĩ is the 4 × 4 unit matrix. This is what one expects, since the eigenvalue of J2 is J(J + 1), which is 15/4 when J = 3/2.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|