


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 22-8-2016
Date: 21-8-2016
Date: 11-8-2016
|
One-Dimensional Coulomb Potential
An electron moves in one dimension and is confined to the right half-space (x > 0) where it has a potential energy
 (i)
(i)
where e is the charge on an electron. This is the image potential of an electron outside a perfect conductor.
a) Find the ground state energy.
b) Find the expectation value ⟨x⟩ in the ground state
SOLUTION
a) Since the electron is confined to the right half-space, its wave function must vanish at the origin. So, an eigenfunction such as exp(-αx) is unsuitable since it does not vanish at x = 0. The ground state wave function must be of the form ѱ = Nx exp(-αa), where α needs to be determined. The operator p2 acting on this form gives
 (1)
(1)
so that using this wave function in Schrodinger’s equation yields
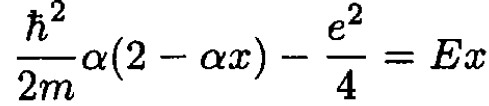 (2)
(2)
For this equation to be satisfied, the first and third terms on the left must be equal, and the second term on the left must equal the term on the right of the equals sign:
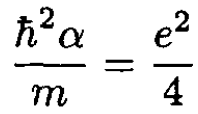 (3)
(3)
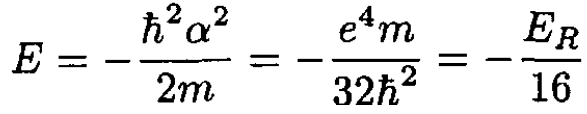 (4)
(4)
The answer is one sixteenth of the Rydberg, where ER is the ground state energy of the hydrogen atom. The parameter α = 1/4a0, where a0 is the Bohr radius.
b) Next we find the expectation value ⟨x⟩. The first integral is done to find the normalization coefficient:
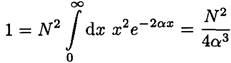 (5)
(5)
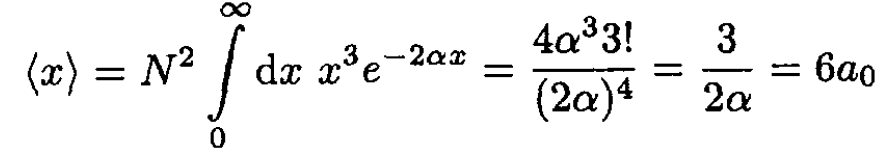 (6)
(6)
The average value of x is 6 Bohr radii.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|