


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | المتجهات في فضاء البعد الثاني وفضاء البعد الثالث-طول المتجه (المعيار): العمليات الحسابية للمتجهات |
|
|
|
أقرأ أيضاً
التاريخ: 7-3-2016
التاريخ: 20-3-2016
التاريخ: 14-3-2016
التاريخ: 29-2-2016
|
طول المتجه (المعيار): العمليات الحسابية للمتجهات:
مبرهنة (1-1) :
لتكن u , v و w متجهات في فضاء 2- وفضاء 3- ، h ، k كميات ثابتة ، فإن الصيغ الآتية تكون متحققة.
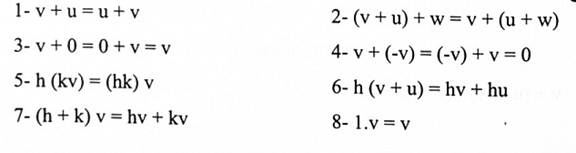
البرهان:
نبرهن العلاقة (2) وتترك البقية كتمارين.
a.الطريقة الهندسية: نفرض أن w,u,v تمثل المتجهات QP , PQ و RS على التوالي [لاحظ الشكل (1-1)].
عليه فإن u + v = QS و v+ (u + w) = PS
كذلك v + u = PR و (v + u) + w = PS
لذا فإن v + (u + w) = (v + u) + w

شكل (1-1)
b.الطريقة الجبرية (التحليلية): نفرض أن المتجهات w , u , v مرسومة في فضاء -3 (بنفس الطريقة في الفضاء 2-). ولتكنv = (v1, v2, v3) و u = (u1, u2, u3)
إذن:

طول المتجه: ليكن v = (v1 , v2) متجه في فضاء 2- v = (v1 , v2 , v3) في فضاء 3-] فإن طول v (معيار v)، يكتب ||v||، ومن نظرية فيثاغورس:
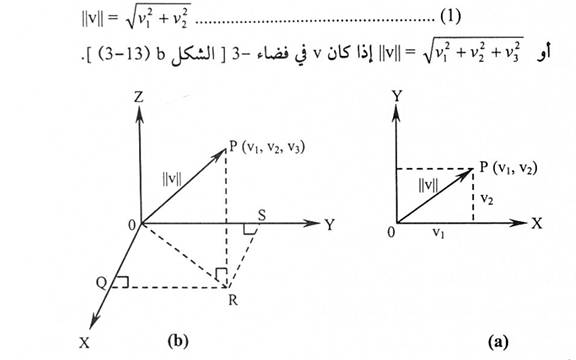
شكل (1-2)
ملاحظة:
المتجه الذي طوله يساوي 1 يسمى متجه الوحدة.
إذا كانت النقطتان P = (v1 , v2, v3) و Q (u1 , u2 , u3) في فضاء 3- فإن المسافة بنهما هي طول المتجه PQ ويكتب:
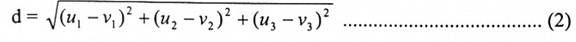
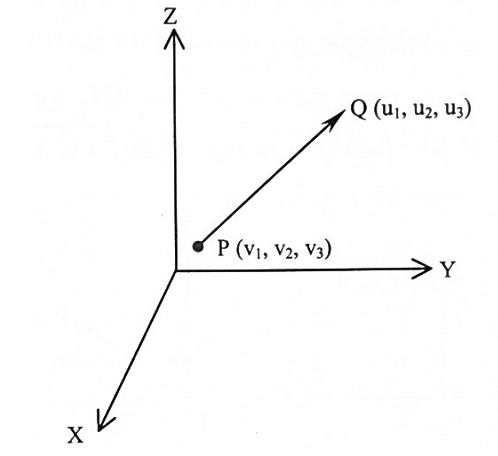
شكل (1-3)
لاحظ أن PQ هو متجه حر حيث أن بدايته لا تقع على نقطة الأصل وعندما P تقع على نقطة الأصل 0 فيسمى بالمتجه المقيد وفي مثل هذه الحالة v1 = v2 = v3 = 0 وبالتعويض في (2) نحصل على:
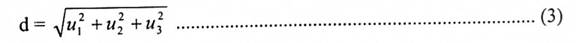
لاحظ [الشكل b (1-2)].
مثال(1):
1. اوجد طول المتجه (v = (-1 , 3 ,2
2. أوجد المسافة PQ حيث P (3,1,-2) و Q (2,-1,1)
الحل:
1. طول المتجه v هو:
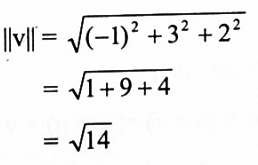
2. المسافة هي:
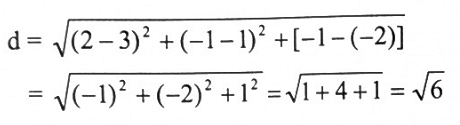
ملاحظة:
من تعريف حاصل ضرب kv، طول المتجه kv، هو:

أي ضرب طول v بالكمية |K| من المرات.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|